Система національних рахунків (2001)

Cтатистичне моделювання макроекономічних показників можна здійснювати за допомогою різних статистичних методів. Найбільш поширеними є кореляційний та регресійний аналіз, але їх застосовують тоді, коли залежність цих показників має стохастичний характер.

У багатьох випадках аналіз може базуватися на ідеї детермінованої (функціональної) залежності результативного показника та факторів, що його формують. Проте, коли ця залежність може бути виражена математичною функцією в явному вигляді (найчастіше у вигляді добутку факторів чи суми добутків), методологію такого аналізу розглядають у рамках теорії статистичних індексів, а самий аналіз називають індексним факторним аналізом.

У макроекономічних моделях найбільш часто за результативну ознаку беруть вартість продукції, а за фактори — витрати капіталу та затрати праці.

Індексний метод. Методику обчислення індексів розглянемо на основі даних про обсяг валової доданої вартості (ВДВ), капітальних вкладень, їх капіталовіддачі за 1996 та 1997 рр. (табл. 6.7).

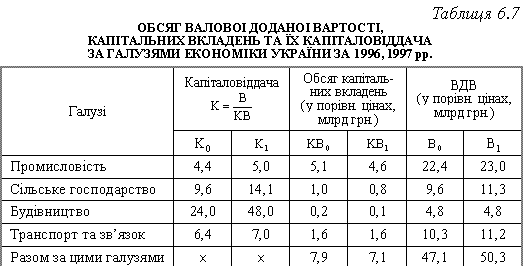
Розрахувавши галузеві індекси, ми отримуємо такі дані за галузями національного господарства (табл. 6.8).

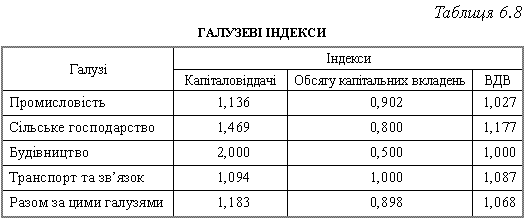
Проаналізувавши ці індекси можна зробити певні висновки про негативну тенденцію зниження обсягу капітальних вкладень та обсягу валового внутрішнього продукту в економіці України, як в цілому, так і за окремими галузями. Індекс капіталовіддачі має також негативну тенденцію до зниження, хоча в таких галузях, як сільське господарство та будівництво спостерігається його зростання.

Використавши дані табл. 6.7, розглянемо методику обчислення та економічний зміст агрегатних індексів. За базисний рік беремо 1996.

Визначаємо зведений індекс загального обсягу валової доданої вартості в цілому в галузях:

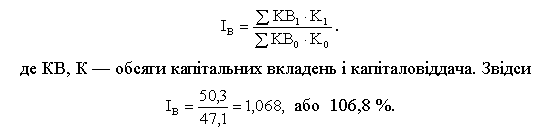
Отже, в цілому ВДВ в галузях економіки в поточному періоді збільшився на 6,8% проти базисного.

Визначаємо зведений індекс капіталовіддачі (інтенсивного фактора):

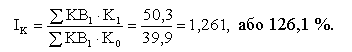
Цей показник свідчить про те, що капіталовіддача в середньому в галузях збільшилась на 26,1%.

Визначаємо зведений індекс обсягу капітальних вкладень (екстенсивного фактора):

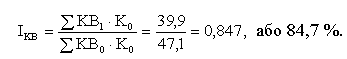
Це означає, що обсяг капітальних вкладень у цілому в усіх галузях зменшився в середньому на 15,3%.

Будуючи агрегатні індекси, треба забезпечувати взаємозв’язок між ними:

,

тобто загальний обсяг ВДВ збільшився на 6,8 % за рахунок обох факторів.

Розкладання абсолютних змін обсягів явищ за факторами. Визначення абсолютної зміни результативного показника за рахунок зміни кожного фактора здійснюється під час побудови системи індексів. Абсолютний приріст за рахунок окремих факторів обчислюють як різницю між чисельником і знаменником відповідних факторних індексів. Так, загальний абсолютний приріст ВДВ (абсолютне зниження) становить:

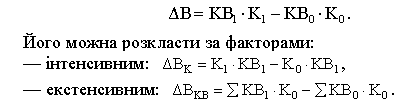
За даними табл. 6.7 обсяг ВДВ у промисловості в поточному періоді (1997 р.) порівняно з базисним (1996 р.) збільшився на 0,6 млрд грн. (23,0—22,4).

Визначимо вплив кожного з факторів на цей показник: за рахунок зміни капітальних вкладень

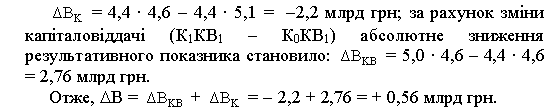
Розкладання абсолютного приросту за факторами на основі зведених індексів здійснюють аналогічно галузевим індексам. Різниця між чисельником і знаменником відповідних індексів зі знаком «+» означає абсолютний приріст, а зі знаком «» — абсолютне зниження. Для системи співзалежних двофакторних зведених індексів у загальному вигляді розкладання абсолютного приросту можна записати так:

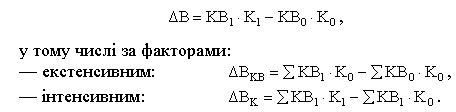
Розрахувавши на основі даних табл. 6.7 загальний зведений індекс обсягу ВДВ за всіма галузями сукупності, бачимо, що абсолютне збільшення обсягу ВДВ у звітному періоді проти базисного за рахунок обох факторів становило 3,2 млрд грн. (50,3  47,1). Далі необхідно визначити як саме кожен з факторів вплинув на загальне скорочення результативного показника.

Так, за рахунок зниження капіталовіддачі в середньому за всіма галузями загальний обсяг ВДВ збільшився на 10,4 млрд грн. (50,3  39,9), а за рахунок зниження іншого фактора, тобто обсягу капітальних вкладень, абсолютне скорочення загального обсягу ВДВ становило 7,2 млрд грн. (39,9  47,1).

Очевидно, що за такого методу розкладання абсолютного приросту за факторами В дорівнюватиме KB + K. Отже, В = = 10,4  7,2 = 3,2 млрд грн.

Підбиваючи підсумки, можна сказати, що ці два фактори, тобто зміна капіталовіддачі та обсягу капітальних вкладень, вплинули на динаміку зниження обсягу ВДВ в 1997 р. проти з 1996 р. в протилежних напрямках. Якщо інтенсивний фактор справляв позитивний вплив, то екстенсивний впливав негативно.

Визначення середньозважених індексів на підставі індивідуальних. Агрегатна форма індексів уможливлює розв’язання багатьох конкретних завдань статистико-економічного аналізу. Економічний зміст чисельника і знаменника будь-якого з таких індексів є достатньо зрозумілим, а тому чітким і прозорим є й зміст самого індексу. Проте в окремих випадках неможливо вивчити динаміку складного економічного явища за цією формою індексу. Тому постає потреба у використанні інших форм зведених індексів (найчастіше арифметичного чи гармонічного). Суть способу визначення середньозважених індексів на підставі індивідуальних полягає в тому, що спочатку для окремих видів продукції (галузей) розраховують індивідуальні індекси, а потім з їхньою допомогою — середній індекс. Без огляду на те, в якій формі розраховується індекс (арифметичній чи гармонічній) кожну з них обов’язково треба брати як зважену, тобто:

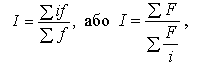
де i — індивідуальний індекс показника, а f і F — вага відповідно в середньоарифметичному і середньогармонічному індексах. Вибір тієї чи іншої форми індекса залежить від цілей його визначення і вихідних даних. Так, якщо треба охарактеризувати зміну екстенсивного показника в середньому за сукупністю різнорідних елементів, використовують середньоарифметичний зважений індекс:

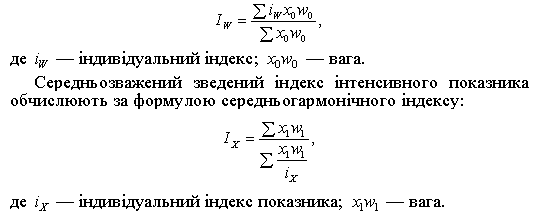
Методику розрахунку середньозважених індексів на підставі індивідуальних розглянемо за даними табл. 6.9.

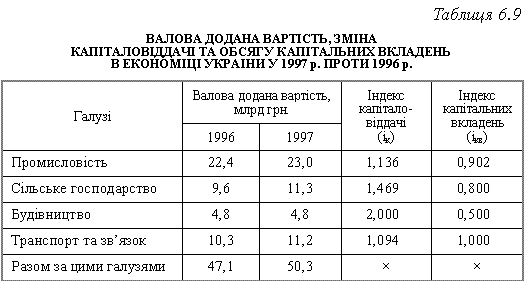
Для вимірювання динаміки екстенсивного показника, тобто обсягу капітальних вкладень у середньому за сукупністю, застосуємо середньоарифметичний зважений індекс:

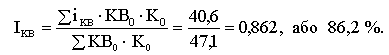
Отже, обсяг капітальних вкладень зменшився у звітному періоді проти базисного в середньому на 13,8 %.

Таке значне зниження обсягу капітальних вкладень щодо сукупності в цілому було спричинене насамперед дуже великим падінням обсягу капітальних вкладень у будівництво та сільське господарство.

Середньозважений зведений індекс інтенсивного показника, тобто капіталовіддачі, обчислюємо за формулою середньогармонічного індексу:

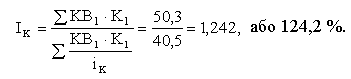
Отже, капіталовіддача в середньому щодо сукупності галузей у звітному періоді проти базисного зросла на 24,2 %. Це зростання сталося насамперед за рахунок значного збільшення капіталовіддачі у промисловості, будівництві, сільському господарстві. Тому можна казати про значний вплив показників промисловості на кінцевий підсумок середньозважених індексів. Це відбувається, головно, тому, що частка ВДВ промисловості в загальному обсязі ВДВ набагато більша за частки інших галузей.

Використання індексів середніх величин. Аналіз динаміки середнього рівня здійснюють на основі побудови взаємозалежних індексів. Індекс, що характеризує зміну середнього рівня інтенсивного показника за рахунок зміни всіх факторів у цілому, дорівнює добутку індексів-співмножників, кожний з яких характеризує зміну лише одного фактора і вплив цієї зміни на динаміку середньої.

Методику розрахунку індексів середніх величин та їх економічний зміст розглядатимемо на прикладі такого інтенсивного показника, як капіталомісткість (табл. 6.10). Показник капіталомісткості розраховується як відношення капітальних вкладень до валової доданої вартості, тобто:

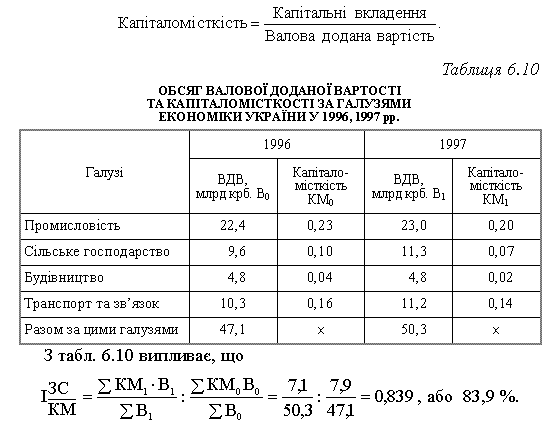
У середньому за всіма галузями капіталомісткість знизилась на 15,6 % за рахунок падіння капіталомісткості в кожній галузі, крім транспорту та зв’язку, де її рівень залишився незмінним.

Вплив структурного фактора визначимо так:

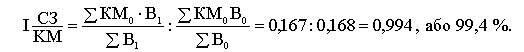
Отже, середня капіталомісткість зменшилась на 0,6 % за рахунок збільшення питомої ваги ВДВ у галузях з більш високим рівнем капіталомісткості: сільському господарстві та будівництві.

Між розрахованими індексами є взаємозв’язок:

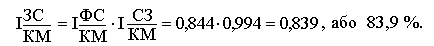
Побудова багатофакторних індексних моделей. В статистиці часто використовується результативний показник, якій залежить від трьох і більше факторів. Тому, вивчаючи динаміку такого складного результативного показника, важливо правильно побудувати систему взаємозв’язаних індексів. Це завдання є складнішим, ніж вивчення взаємодії двох факторів, оскільки визначаючи вплив одного з трьох факторів на зміну результативного показника необхідно фіксувати як незмінні два інші фактори, кожний з яких фіксується на різних рівнях.

Проаналізуємо динаміку капітальних вкладень в економіці України на основі адитивно-мультиплікативної багатофакторної системи індексів. Використаємо дані табл. 6.11.

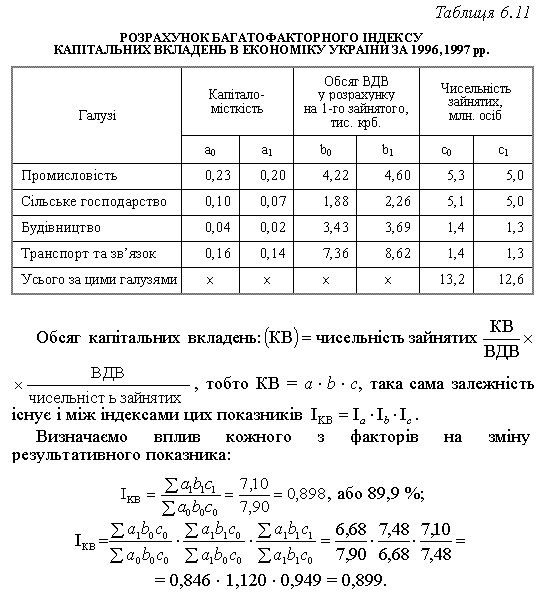
Отже, обсяг капітальних вкладень знизився на 10,1 % за рахунок усіх факторів.

Можна зробити висновок, що за рахунок зміни капіталомісткості обсяг капітальних вкладень зменшився на 15,4 %, за рахунок зміни обсягу ВДВ на одного зайнятого збільшився на 12,0 %, за рахунок зміни чисельності зайнятих зменшився на 5,1 %, а за рахунок всіх трьох факторів зменшився на 10,1 %.

Наступним етапом аналізу буде визначення впливу кожного фактора в абсолютних значеннях на зміну обсягу капітальних вкладень.

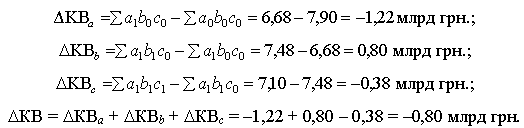
Можна зробити висновок про те, що абсолютний обсяг капітальних вкладень зменшився у 1997 р. проти 1996 р. на 0,80 млрд грн. У тому числі: за рахунок зміни капіталомісткості обсяг капітальних вкладень зменшився на 1,22 млрд грн., за рахунок зміни ВДВ на одного зайнятого — збільшився на 0,8 млрд грн., за рахунок зміни чисельності зайнятих — зменшився на 0,38 млрд грн.

Кореляційний метод. У більшості економічних досліджень необхідно вивчати динаміку кількох показників одночасно, тобто розглядати паралельно кілька динамічних рядів. Природно, що в цих випадках можна натрапити на ряди, що в них коливання рівнів є взаємозумовленими. У процесі вивчення такого роду рядів динаміки може постати необхідність виміряти залежність між рядами, тобто визначити, наскільки коливання рівнів одного ряду залежать від коливання рівнів іншого ряду. Ця задача розв’язується корелюванням рядів динаміки, тобто обчисленням коефіцієнта кореляції.

Під час вивчення кореляційних зв’язків у багатомірних динамічних рядах виникають певні методологічні складності, спричинені їх автокореляцією. Наявність автокореляції порушує одну з умов регресійного аналізу — незалежність спостережень, і призводить до викривлення його результатів. У практиці статистично-економічного аналізу застосовують різні способи усунення автокореляції. Один з цих способів полягає у запровадженні змінної величини t в рівняння регресії Y = F(x1, x2 ... xt), де вона виконує роль фактора часу. Методику побудови такого рівняння регресії можна розглянути на прикладі двох взаємозв’язаних рядів динаміки (табл. 6.12): валового внутрішнього продукту (ВВП) (yt) і капітальних вкладень в економіку України (xt). Зв’язок між цими показниками можна відобразити лінійною функцією:

Yt = a0 + a1x + a2t ,

де a1 — параметр, який характеризує середній приріст результативної ознаки Y на одиницю приросту факторної ознаки Y, a2 — середній щорічний приріст Y під впливом зміни комплексу факторів, крім x.

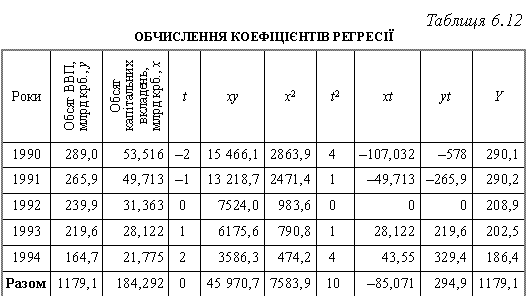
Визначимо параметри функції Yt = a0 + a1x + a2t. Параметри функції визначають методом найменших квадратів, система нормальних рівнянь складається традиційно:

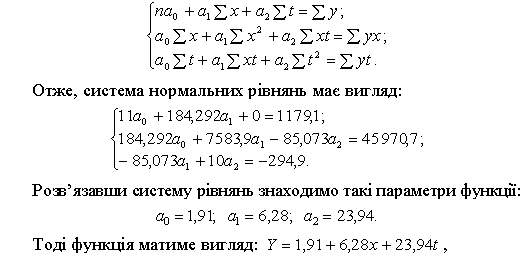
тобто підвищення обсягу капітальних вкладень в економіку України на 1 грошову одиницю веде до збільшення ВВП на 6,28 грошових одиниць.

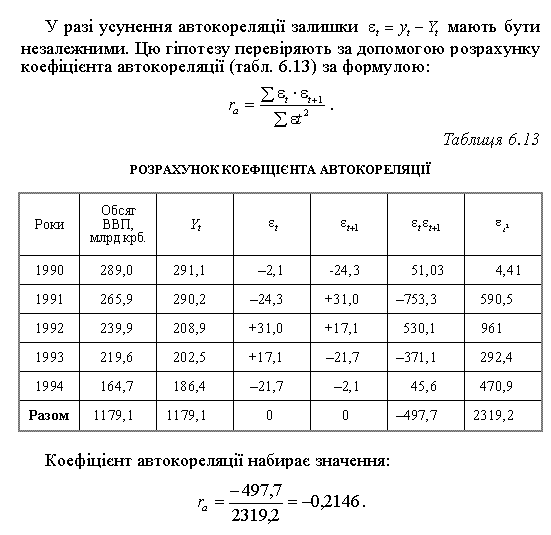
Для перевірки автокореляції в залишкових величинах можна використовувати критерій Дарбіна-Ватсона, який позначається символом d і розраховується за формулою: