Мікроекономічна теорія виробництва і витрат (2003)

Виробнича функція короткострокового періоду не обов’язково має такий вигляд, як це показано на рис. 2.1 і 2.2. Розглянемо інші види короткострокових функцій виробництва і притаманні їм властивості.

Постійна віддача змінного ресурсу. Деякі виробничі процеси характеризуються постійною віддачею змінного ресурсу, тобто кожна наступна одиниця змінного ресурсу, додана до постійних ресурсів, приводить до такого самого збільшення випуску, як і попередня. У цьому разі загальний продукт зростає рівномірно, а граничний і середній продукти є постійними. Така виробнича функція описується лінійним рівнянням

Q=a+bx, (2.9)

де Q — обсяг випуску продукції в натуральному вимірі за розрахунковий період часу;

x — кількість спожитого за той самий період змінного ресурсу;

а та b — параметри рівняння.

Якщо зроблено допущення, що змінний ресурс абсолютно важливий для виробництва і результат (загальний продукт) може бути отриманий відразу ж після поєднання змінного ресурсу з постійними, виробнича функція виходить із початку координат і значення параметра а дорівнює 0. У такому разі рівняння (2.9) спрощується і має вигляд:

Q=bx (2.10)

У графічному вигляді таку функцію наведено на рис 2.3.

Не слід уважати, що лінійна виробнича функція суперечить закону спадної віддачі змінного фактора, — точка, починаючи з якої віддача почне знижуватися, ще не досягнута. Для багатьох видів виробництв вона відповідає приблизно 95—100 % від рівня використання виробничих потужностей. Розглянемо такий приклад. Сім’я розмальовує дерев’яні ложки, використовуючи власне помешкання, при цьому виробіток будь-якого члена сім’ї за добу однаковий. Зрозуміло, що чим більшою буде кількість членів сім’ї, які щодня займатимуться роботою, тим більшим буде й загальний продукт. Обмежувальним ресурсом є площа помешкання, розрахована, наприклад, на 5 осіб. Якщо в цьому помешканні розмістити більшу кількість працівників, то вони заважатимуть один одному.

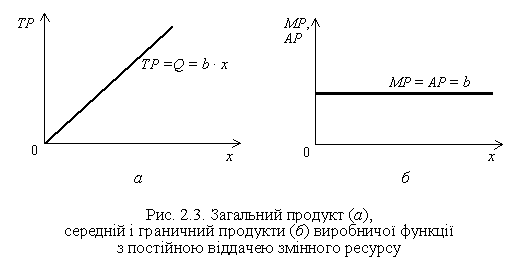
У промисловості постійна віддача характерна для виробництв, де дотримуються стандартні співвідношення між робітниками і верстатами, агрегатами та обслуговуючим персоналом. Умовою постійної віддачі змінного ресурсу є подільність постійного ресурсу за збереження його однорідності.

Зростаюча віддача змінного ресурсу. Для виробничої функції такого виду кожна наступна одиниця змінного ресурсу дає більший приріст загального продукту, ніж попередня. Така функція виробництва задається рівнянням

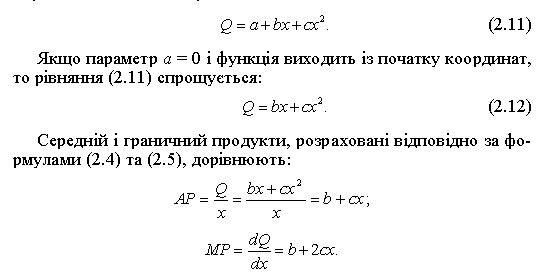
Графічно цю функцію наведено на рис. 2.4.

Позитивний знак параметра с обумовлює ту обставину, що параболічна крива (рис. 2.4, а) увігнута до осі ординат, і отже, ні загальний продукт ТР, ні граничний продукт МР, ні середній продукт АР не досягають максимуму. Таким чином, квадратична виробнича функція з позитивним параметром с, здавалося б, цілком суперечить закону спадної віддачі змінного ресурсу. Але це не так. Просто для багатьох виробничих процесів вона описує початкову стадію освоєння випуску продукції, коли до створеного виробничого апарату, тобто до визначеної кількості постійних ресурсів, починають додавати змінний ресурс і кожна його додаткова одиниця, змінюючи пропорцію суміші, вносить все більшу частку в сукупний продукт, у результаті чого й темпи його випуску зростають. Зрозуміло, що раніше або пізніше виробництво вийде на проектну потужність, і далі діятиме принцип спадної віддачі змінного фактора. Рівняння (2.11) або (2.12) дають змогу математично точно описати деяку ділянку будь-якої виробничої функції за малих обсягів застосування змінного фактора виробництва.

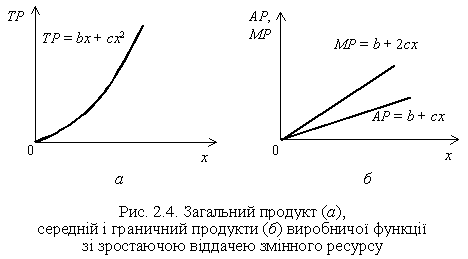
Спадна віддача змінного ресурсу. Виробнича функція такого виду демонструє спад віддачі відразу ж після використання першої одиниці змінного ресурсу (розуміється, в сукупності з постійними ресурсами), тобто кожна наступна одиниця змінного ресурсу дає менший приріст загального продукту, ніж попередня. Така функція задається квадратичним рівнянням з негативним параметром с:

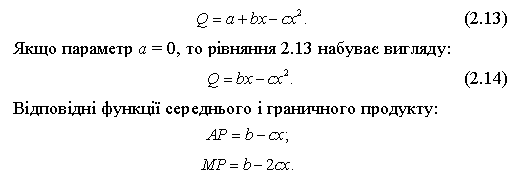
Графік такої функції наведено на рис. 2.5.

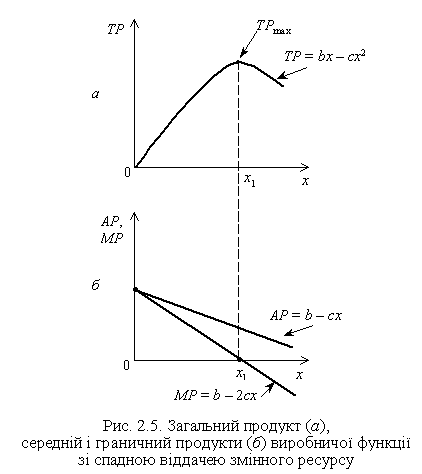
Негативний знак параметра с обумовлює увігнутість параболи (рис. 2.5, а) до осі абсцис, тобто загальний продукт з кожною додатковою одиницею змінного ресурсу збільшується все в меншому ступені. Він досягає максимуму за використання х1 одиниць змінного фактора, при цьому постійні ресурси задіяні в максимальному ступені, отже, неможливо досягти більшого обсягу випуску без їх збільшення. Середній і граничний продукти максимальні для першої одиниці змінного ресурсу (зауважимо, що на рис. 2.3  2.5 розмірність осі х починається з одиниці), потім граничний продукт змінного ресурсу зменшується, хоча й залишається позитивним до досягнення змінним ресурсом значення х1. Оскільки додаткові одиниці змінного ресурсу знижують граничний продукт і, отже, знижують темпи приросту загального продукту, остільки знижується й значення середнього продукту. Лінія АР — пряма, що спадає та відтинає на осі ординат відрізок b (до речі, так само, як і лінія МР), причому її нахил у два рази менший за нахил лінії МР, і вона на всій області розміщена вище лінії МР.

Це більш реальний випадок. Саме така природа багатьох виробничих процесів дала змогу виявити феномен короткострокового періоду — спадну віддачу змінного ресурсу і навіть увести його в ранг закону.

Різні види віддачі змінного фактора добре описуються, крім наведених рівнянь, степеневою виробничою функцією

Якщо а = 1 кривизна функції визначається кількісним значенням параметра b. Виробнича функція характеризується віддачею (див. рис. 2.6): якщо b = 1 — постійною; b > 1 — зростаючою; якщо b < 1 — спадною.

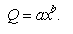
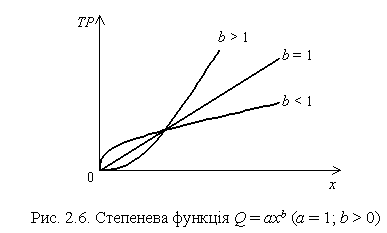
Короткострокова функція виробництва узагальненого вигляду. Криві загального, середнього і граничного продукту, наведені на рис. 2.1, 2.2, добре ілюструють традиційну, або класичну, виробничу функцію з одним змінним фактором, її параметри та їх взаємозв’язки докладно розглянуто у попередньому параграфі. Така виробнича функція описується кубічним рівнянням

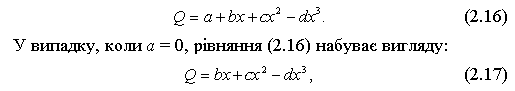
де b, c, d — постійні параметри рівняння.

Кубічна виробнича функція добре відображує як зростаючу, так і спадну віддачу змінного ресурсу, тому її часто називають короткостроковою функцією виробництва загального вигляду.

Середній і граничний продукти у цьому випадку описуються квадратичними функціями

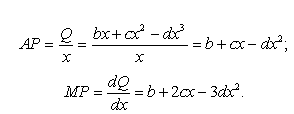
Оскільки параметр d у виробничій функції загального вигляду від’ємний, граничний продукт змінного ресурсу спочатку збільшується, досягає максимуму, потім зменшується. Максимуму МРх відповідає точка перегину кривої ТР. До точки перегину крива ТР увігнута до осі ординат (зростаюча віддача), після точки перегину — вона увігнута до осі абсцис (спадна віддача).

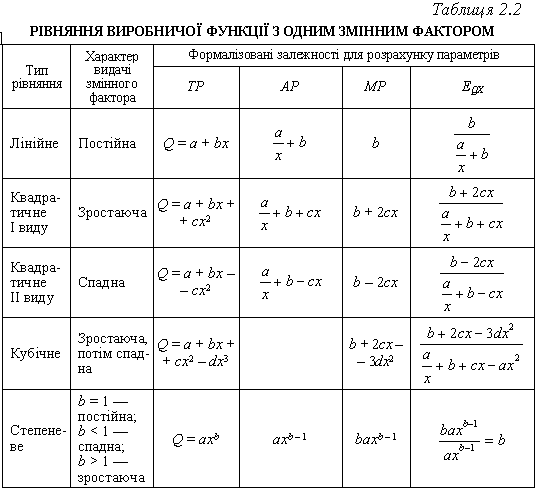
У табл. 2.2 узагальнено всі розглянуті випадки і наведено рівняння, за допомогою яких можна описати взаємозв’язок у системі «витрати—випуск» за експериментального дослідження виробництва з одним змінним фактором і різними видами його віддачі.

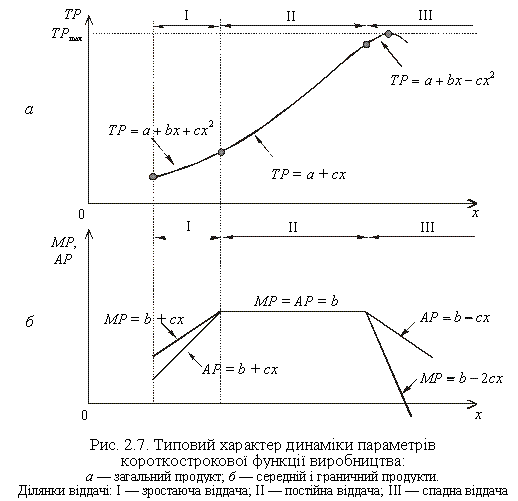
Зауважимо, що результати численних досліджень і за галузями, і за видами продукції показують, що зростаюча віддача спостерігається лише в період освоєння випуску нової продукції. Після виходу підприємства на проектний рівень випуску віддача, як правило, постійна і лише потім, якщо у виробництво продовжують залучати змінний фактор, починає знижуватися. У такому разі конфігурація кривих ТР, АР, МР і взаємозв’язок цих параметрів мають вигляд, як це показано на рис. 2.7.

Короткострокова функція виробництва з кількома змінними факторами. Для багатьох виробництв випуск у короткостроковому періоді є функцією кількох змінних. У сільському господарстві, наприклад, як постійний ресурс виступає, як правило, земля, а як змінні ресурси — добрива, праця, погодні умови, механоозброєність праці і т. ін. У промисловому виробництві постійні фактори — земельна ділянка, на якій розташовано підприємство, будинки, споруди, коштовне спеціальне устаткування і т. ін., а змінні — праця, безпосередньо затрачена на виготовлення продукції, сировина і матеріали, що входять до складу продукції, витрати палива та енергії на технологічні потреби тощо.

У цьому разі короткострокова функція виробництва в загальному вигляді записується так:

Q=f(x1,x2,x3, …, xi, …, xn) (2.18)

Головна задача дослідження короткострокової функції виробництва з кількома змінними ресурсами — як розподілити величину загального продукту між окремими ресурсами виробництва, що, діючи спільно (а є ще й постійні ресурси!), виробляють цей продукт. Або іншими словами: як виміряти внесок кожного ресурсу в кінцевий результат?

Граничний продукт за певним змінним ресурсом, наприклад х1, знаходять шляхом визначення впливу на випуск обсягу застосування ресурсу х1 за фіксованих інших змінних ресурсів (х2, х3, ..., хn). Математично ця процедура означає взяття часткової похідної від функції виробництва по х1. Припустимо, що виробнича функція короткострокового періоду має вигляд:

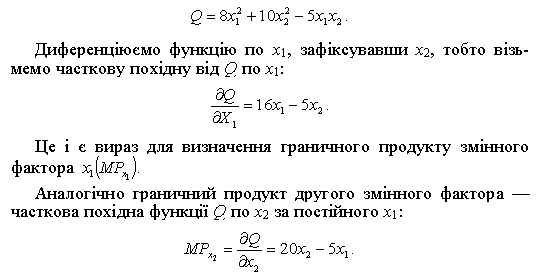
Отже, незалежно від того, яким видом математичного рівняння описується конкретний виробничий процес, скільки незалежних змінних ресурсів включено у виробничу функцію, гранична продуктивність (віддача) конкретного змінного ресурсу (хі) визначається шляхом взяття часткової похідної від загального продукту MPx2:

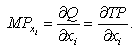
Середній продукт і-го змінного фактора та еластичність випуску за будь-яким змінним ресурсом визначаються за формулами (2.4) та (2.8).