Кількісні методи в управлінні інвестиціями (2000)

Коли фірма оцінює альтернативні проекти, виникають дві проблеми:

можливість виникнення конфлікту при ранжируванні проектів з використанням методів ЧТВ, ВСП і ІП;

коли конфлікт все таки виник, якому методу віддати перевагу для того, щоб забезпечити максимальні прибутки акціонерам?

Справді, під час оцінки альтернативних інвестиційних проектів може виникнути конфлікт у таких випадках:

(1) якщо існує невідповідність у розмірі первинних інвестицій;

(2) якщо проекти мають різні грошові надходження від інвестицій у часі;

(3) якщо проекти мають нерівні терміни існування.

Розглянемо три графіки ЧТВ.

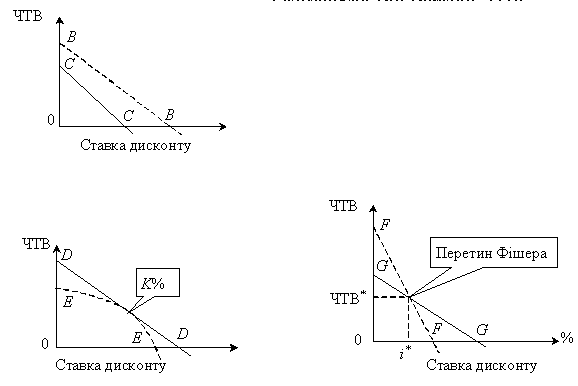
Проект B переважає проект С за критерієм ЧТВ для всіх можливих ставок дисконту. Проект B також має більше значення ВСП.

Графіки ЧТВ проектів Е та D мають спільну точку при ставці дисконту K%. Але ЧТВ проекту D при решті ставок дисконту вища, ніж проекту Е. ВСП проекту D також буде вищою.

ВСП проекту G вища за ВСП проекту F, тому за цим критерієм проект G кращий. При ставках дисконту 0  k < i* ЧТВ проекту F перевершує ЧТВ проекту G, при k = i*ЧТВ обох проектів рівні, при k > i*ЧТВ проекту G перевершує ЧТВ проекту F. У цьому разі виникає конфлікт під час ранжирування альтернативних проектів за методами ЧТВ і ВСП.

Перетин графіків ЧТВ проектів при ставці дисконту k = i*, коли ЧТВ обох проектів рівні, називається перетином Фішера, на честь американського економіста Ірвінга Фішера, який обґрунтував даний випадок перетину графіків ЧТВ проектів у своїх роботах «Процентна ставка» і «Теорія процента», опублікованих відповідно в 1907 і 1930 рр.

Визначимо ставку дисконту i*, при якій виникає перетин Фішера на графіках ЧТВ двох альтернативних проектів (назвемо їх А і В). Тоді NPVА = NPVВ.

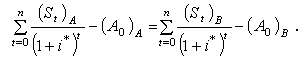
Дане рівняння може бути спрощене, якщо члени правої частини рівняння перенести в ліву частину. Тоді методика обчислення нічим не відрізнятиметься від методики обчислення ВСП.

Може виникнути конфлікт в оцінках між методами ЧТВ і ІП при існуванні невідповідності між проектами за розмірами первинних інвестицій, а також між методами ІП і ВСП, якщо методи ЧТВ і ІП узгоджуються в ранжуванні проектів.

Нехай NPVJ — ЧТВ проекту J, а СJ — теперішня вартість інвестицій у проект J, J = 1, 2. Якщо NPV1 > NPV2 , то за критерієм ЧТВ проект 1 переважатиме. Якщо ж NPV1 / NPV2 < C1/C2, то існує конфлікт між методами ЧТВ і ІП при ранжуванні проектів. Для того, щоб це показати, перетворимо наведену вище нерівність:

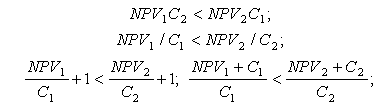
Звідки PI1 < PI2.

● Приклад 1. Перетин Фішера

Фірма оцінює два альтернативні проекти:

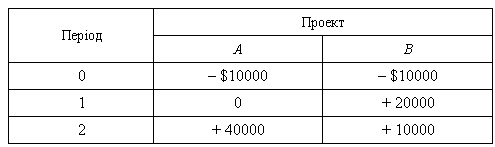
Розрахувати:

(1) ВСП кожного проекту;

(2) чи можна за результатами розрахунку ВСП і за грошовими потоками проекту сказати про наявність перетину Фішера, чи ні?

(3) обчислити ставку дисконту в точці перетину Фішера і ЧТВ обох проектів.

Розв’язання. (1) Обчислимо ВСП проектів, позначивши їх як IRRA і IRRB за формулою (4.1):

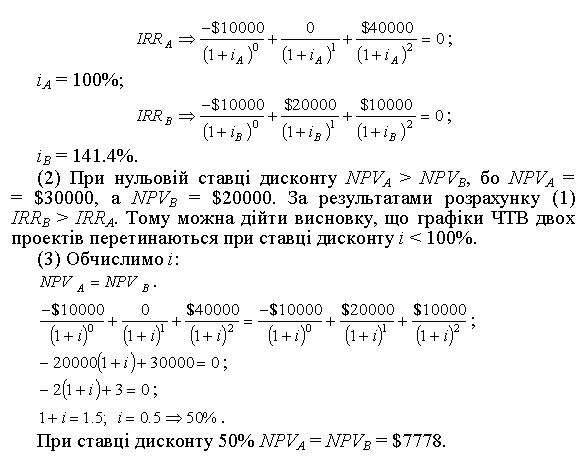
На графіку видно, що при будь-якій процентній ставці i < 50% модель ЧТВ віддаватиме перевагу проекту А, в той час як модель ВСП — проекту В. При ставці i > 50% обидві моделі визначать найкращим проект (В).

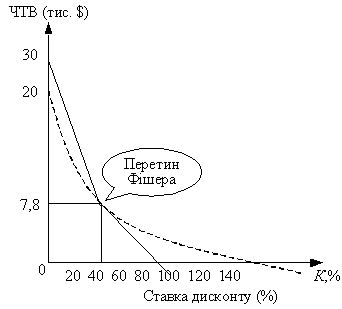
Рішення прикладу 1 показало, що при необхідній ставці прибутковості k < 50% виникає конфлікт у ранжуванні проектів за критеріями ЧТВ і ВСП. Який з проектів все ж таки вибрати? Розглянемо додатково кілька прикладів, що допоможуть це зробити.

● Приклад 2. Порівняння методів ЧТВ та ВСП

Нехай фірма має вартість капіталу 16%. Грошові потоки проектів А і В взяті з прикладу 1. Оскільки грошові надходження проекту А в період 1 дорівнюють 0, то для того, щоб привести обидва проекти до еквівалентного вигляду, фірма мала намір узяти позику в кінці періоду 1 в сумі $20000 під 16% річних, тобто рівній грошовим надходженням проекту В в період 1, з поверненням основної суми з процентом наприкінці періоду 2. Фірма розрахувала таку таблицю.

Проект (А) + Позика перевершує проект (В) за грошовими надходженнями в період 2 ($16800 проти $10000) при однаковій можливості інвестувати $20000 в кінці періоду 1. Тому, враховуючи еквівалентність проектів (А) і (А)+Позика, можна зробити висновок, що проект (А) бажаніший, ніж проект (В) при будь-якій ставці, меншій за 50%.

● Приклад 3. Порівняння методів ЧТВ та ВСП

Фірма, що має вартість капіталу 10 %, оцінює проекти А і В таким чином:

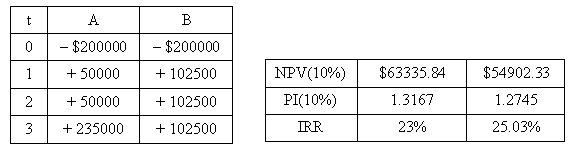
Моделі ЧТВ і ІП ранжують вище проект А, а ВСП — проект B. Припустимо, що фірма зможе отримати позику на суму $200000, рівну сумі первинних інвестицій обох проектів за необхідною процентною ставкою (10%) на три роки за умови, що в кінці кожного року фірма направлятиме на покриття основної суми позики і виплату процентів за позикою грошові надходження від проектів.

Фірма розрахувала такі дві таблиці:

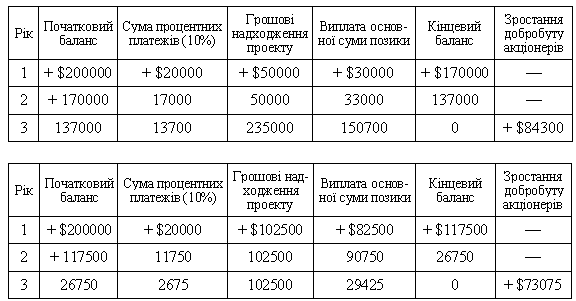
З таблиць видно, що проект А збільшує добробут акціонерів на $84300 порівняно з проектом В — $73075. Якби фірма під час вибору проекту використала критерій ВСП і вибрала проект В, то це призвело б до втрати $11225 в кінці 3-го року.

Тож можна вивести важливе співвідношення між сумою збільшення добробуту акціонерів у кінці 3-го року кожного проекту і їхньою ЧТВ. Якщо суму зростання добробуту акціонерів дисконтувати зворотно до періоду 0 за необхідною фірмі ставкою прибутковості інвестицій, отримаємо точну величину ЧТВ проекту, тобто:

● Приклад 4. Порівняння методів ЧТВ та ВСП

Складемо ще одну таблицю, використовуючи дані прикладу 3.

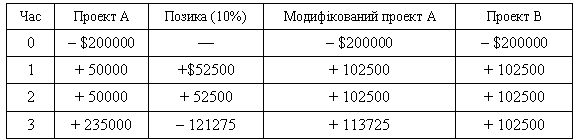
Сума виплат за позикою — $121275 = $52500 (1.1)2+ + $52500 (1.1).

Грошові надходження модифікованого проекту А більші від грошових надходжень проекту В ($113725 і 102500) у кінці 3-го року. Тож, проект А ліпший.