Кількісні методи в управлінні інвестиціями (2000)
8.2. ОПТИМІЗАЦІЯ РОЗПОДІЛУ ІНВЕСТИЦІЙНИХ РЕСУРСІВ МІЖ ПРОЕКТАМИ
Задача розподілу інвестиційних ресурсів між проектами в термінах лінійного програмування записується таким чином:
Максимізувати
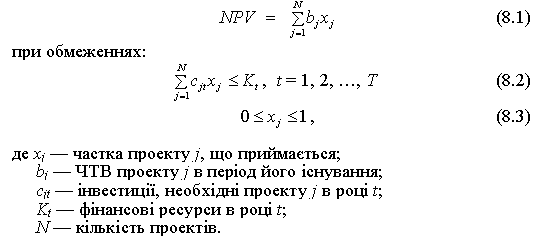
Фірма хоче вибрати множину проектів, які мали б максимальну сумарну ЧТВ за умови додержання всіх обмежень.
Тут слід зазначити, що в даному формулюванні задачі розподілу інвестицій між проектами в термінах лінійного програмування:
дозволяється приймати частину проекту, тому що змінна xj — неціла;
використання обмеження невід’ємності xj (0 xj 1) показує вищий ліміт кожного проекту, тобто кожен проект може мати максимальну частку, що дорівнює 1, або що він приймається на 100%;
передбачається, що всі вхідні параметри — bj, cjt та Kt — ОПІР оцінює в умовах визначеності;
параметр bj показує ЧТВ проекту j упродовж терміну його існування, де всі грошові потоки дисконтуються за вартістю капіталу фірми;
● Приклад 1. Постановка задачі оптимального розподілу фінансових ресурсів між інвестиційними проектами
Фірма має портфель, що складається з 9 проектів. Вона оцінила ЧТВ і обсяги інвестування кожного проекту упродовж 2 років таким чином:
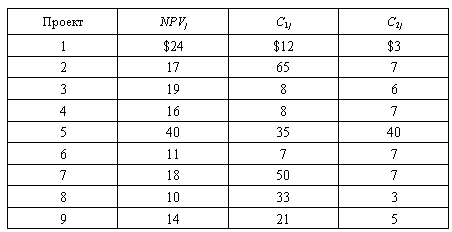
Але фірма має обмежені фінансові ресурси для інвестування проектів: на рік 1 — $150, на рік 2 — $40. Сформулюйте задачу оптимального розподілу інвестицій між проектами в термінах лінійного програмування.
Розв’язання.
Постановка цієї задачі в термінах лінійного програмування формулюється таким чином:
Максимізувати
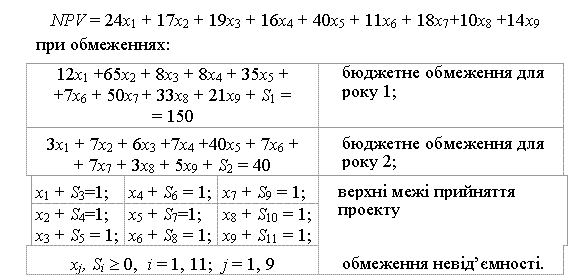
Штучні змінні S1 і S2 являють собою кількість бюджетних коштів за 1 та 2 роки відповідно, що залишаються нерозподіленими в будь-який з 9 проектів.
Штучні змінні з S3 по S11 являють собою частки проектів 1—9 відповідно, що не приймаються фірмою.
Pозглянемо модифіковану постановку задачі оптимального розподілу інвестицій між проектами. Сенс модифікації полягає в тому, що крім бюджетних обмежень по періодах та обмежень на прийняття проектів, вводяться додаткові обмеження, наприклад, на обіговий капітал — W, управлінські витрати — M, витрати на екологію тощо.
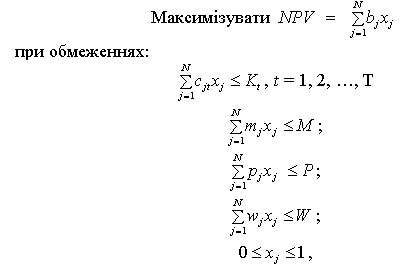
де xj — частка проекту j, що приймається;
bj — ЧТВ проекту j в період його існування;
Kt — інвестиційні ресурси в році t;
N — кількість проектів;
wj — обіговий капітал для проекту j;
mj — управлінські витрати на проект j;
pj — витрати на охорону навколишнього середовища проекту j;
W — обіговий капітал;
М — управлінські витрати;
Р —витрати на охорону навколишнього середовища.
Двоїста задача оптимізації розподілу інвестицій між проектами в термінах лінійного програмування дає важливу інформацію фінансовому менеджеру в процесі прийняття інвестиційних рішень.
Загальне формулювання двоїстої задачі, що відповідає формулюванню основної задачі (8.1)—(8.3), є таким:
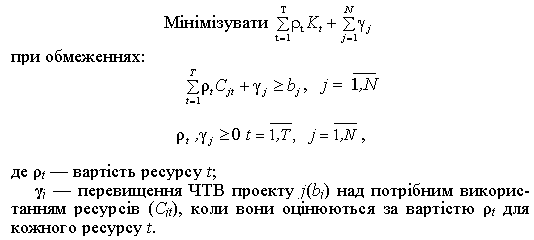
Задача цілочисельного програмування
Основні причини використання цілочисельного програмування (ЦП) для розв’язання задачі оптимального розподілу інвестицій між проектами полягають ось у чому:
Труднощі, що виникають при прийнятті часткових інвестиційних проектів, як це було в задачі лінійного програмування, зникають, бо цілочисельне програмування потребує, щоб проекти приймались або цілком, або відхилялися;
Всі взаємозалежності між проектами можуть бути включені до обмежень задачі цілочисельного програмування, в той час як це неможливо зробити в задачі лінійного програмування через існування часткових проектів.
Загальна постановка задачі:
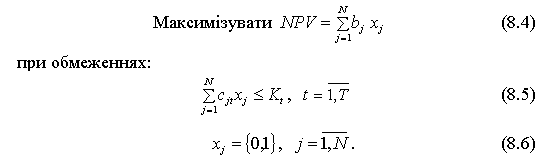
На відміну від формулювання задачі лінійного програмування, в цій постановці Xj набувають цілих значень 0 або 1. Якщо Xj = 1, то проект приймається, якщо Xj = 0 — відхиляється.
При використанні простих моделей оцінки інвестиційних проектів — ЧТВ, ВСП та ІП — припускалося, що всі інвестиційні проекти незалежні один від одного, тобто грошові потоки проектів не взаємопов’язані між собою, не впливають або не змінюють потоки один одного при прийнятті деяких з них.
У розділі 3 відзначалися три види залежностей між проектами — альтернативні, доповнюючі та залежні.
Альтернативні проекти — це проекти, прийняття одного з яких виключає прийняття будь-якого іншого.
В задачі ЦП існування таких проектів описується обмеженням:
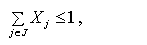
де J — множина альтернативних проектів.
Це обмеження показує, що або лише один проект обирається з множини J, або жоден. Але якщо потрібно вибрати все-таки один проект з множини проектів J, то обмеження записується як:
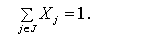
Важливим застосуванням даного обмеження є ситуація, коли фірма бажає відкласти прийняття проекту на один чи більше років. Розглянемо приклад.
Нехай є проект Х з грошовими потоками
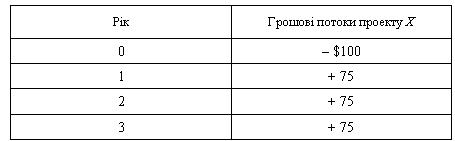
ЧТВ проекту при ставці дисконту 10% дорівнює $86.51. Якщо фірма хоче визначити, чи бажано відкласти прийняття проекту на 1 або 2 роки, необхідно ввести два нові варіанти проекту Х-проекту Х1 та X2:

ЧТВ проектів Х1 та Х2 при вартості капіталу фірми 10% дорівнюватимуть відповідно $78.66 та $ 71.50.
Для того, щоб вибрати один з трьох варіантів проекту, необхідно записати таке обмеження:
Х1 + Х2 + Х = 1.
Залежні проекти — це такі проекти, прийняття одного з яких обумовлює попереднє прийняття інших проектів. Наприклад, якщо проект А не приймається без попереднього прийняття проекту В, то проект А є залежним від проекту В. Така залежність описується обмеженням:
ХА ХВ. (8.9)
● Приклад 2. Обмеження, що описують взаємозалежність між проектами в задачі ЦП
Сформулювати відповідні обмеження задачі ЦП для кожного з випадків:
1. Два проекти (6) і (8) є альтернативними, а третій проект (16) є залежним від даних проектів і повинен бути прийнятий або за умови прийняття проекту (6), або (8).
2. Проект (10) не приймається , якщо не будуть прийняті проекти (7) і (9).
3. Якщо з множини альтернативних проектів (1), (2), (3), (4) і (5) не більше трьох будуть прийняті, то проект (11) приймається за умови, що з даної множини проектів будуть прийняті не більше двох, а проект (14) — коли не більше трьох.
Розв’язання.
Визначаються два обмеження:
— альтернативність проектів (6) і (8)

Останній тип проектів — доповнюючі проекти, тобто такі, коли прийняття одного проекту впливає на грошові потоки одного або більше проектів.
Припустимо, що є два взаємно доповнюючих проекти (7) і (8). Будь-який з цих проектів може бути прийнятий окремо, однак якщо обидва вони прийматимуться, то інвестиції меншають, а грошові надходження зростають.
Для розв’язання проблеми слід ввести новий проект, наприклад (78), який матиме первинні інвестиції в розмірі 90% від сумарних інвестицій у проекти (7) і (8), а ЧТВ — у розмірі 115% від суми ЧТВ обох проектів. Крім того, треба виключити прийняття одночасно обох проектів (7) і (8) і проекту (78), який є об’єднанням перших двох:
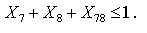
Розглянемо складніший приклад, що продемонструє можливості формування оптимального портфеля інвестиційних проектів за допомогою задачі ЦП.
● Приклад 3. Повне формулювання задачі ЦП
Фірмі потрібно сформувати оптимальний портфель інвестиційних проектів. Вона оцінює 12 інвестиційних проектів з життєвим циклом 3 роки.
Фірма має обмеження на обсяги щорічного інвестування цих проектів: у 1-й рік обсяг інвестицій в проекти не повинен перевищувати $250 тис., у 2-й рік — $450 тис., у 3-й рік — $300 тис.
Між проектами існують такі взаємозв’язки:
1. З множини проектів 5, 7 і 9 можна прийняти два;
2. Проекти 4 і 8 є альтернативними, але один з них потрібно прийняти;
3. Проект 11 не приймається без прийняття проектів 1 та 3;
4. Проект 1 може бути відкладений на 1 рік за умови незмінності обсягів інвестування, але ЧТВ при цьому зменшиться до $30 тис.;
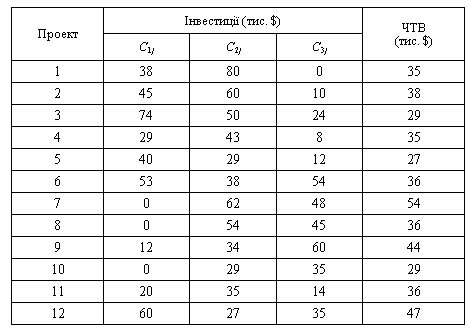
5. Проекти 2 і 7 та проекти 10 і 12 розглядаються як об’єднані, причому загальні інвестиції зменшуються на 15%, а ЧТВ збільшується на 10% у порівнянні з сумарними показниками окремих проектів;
6. Хоча б один з об’єднаних проектів доцільно прийняти.
Сформулюйте задачу визначення оптимального портфеля інвестиційних проектів у термінах ЦП.
Розв’язання.
Вводимо три нові змінні:
Х13 — для визначення відкладення проекту 1 на 1 рік;
Х14 — для визначення об’єднаних проектів 2 і 7;
Х15 — для визначення об’єднаних проектів 10 і 12.
Тепер сформулюємо задачу ЦП:


Можливість включення обмежень для опису взаємозв’язків проектів робить постановку задачі ЦП реалістичнішою, ніж задачі ЛП. Але незважаючи на незначні зміни в постановці (вимога цілочисельності), алгоритми розв’язання задачі ЦП значно складніші та довші в часі.