Економічний ризик: ігрові моделі (2002)

Нехай аграрне підприємство (перший гравець) може посіяти одну з трьох культур. Його стратегії позначимо через s1, s2, s3. Необхідно визначити, яку з культур сіяти, якщо за інших рівних умов урожаї цих культур залежать, головним чином, від погоди (Ө), а план посіву має забезпечити найбільший дохід. Уважатимемо, що сільськогосподарське підприємство має надійний спосіб прогнозування погоди. Визначаємо для другого гравця (“погода”) такі стани (стратегії): Ө1 — рік посушливий; Ө2 — рік нормальний; Ө3 — рік дощовий.

Нехай на основі досвіду відомо, що за сухої погоди з 1 га можна зняти hk1 центнерів культури sk за нормальної — hk2, за дощової — hk3 (k = 1, 2, 3,). Нехай також відомі ціни: ck — ціна 1ц культури sk (k = 1, 2, 3,) в умовних грошових одиницях (УГО). Приймемо, що:

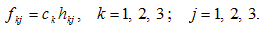
Якщо знехтувати вартістю насіння і витратами на обробіток ґрунту, отримуємо функціонал оцінювання

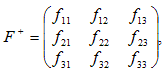
тобто матрицю валових доходів підприємства від реалізації своєї продукції з 1 га за всіх можливих ситуацій. Нехай гра не має сідлової точки і перший гравець (аграрне підприємство) має хоча б одну оптимальну змішану стратеію sp*, що визначається вектором.

Якщо V* — ціна гри, то згідно з (додаток до розділу 1, пункт 1.8.1) для змішаної стратегії P* виконується нерівність:

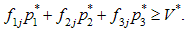
Очевидно, що ціна гри V* (число, яке знаходиться у лівій частині нерівності є величиною очікуваного валового доходу з 1 га за j-го стану погоди, якщо підприємство p1*-ту частку 1 га засіє культурою s1, p2*-ту частку 1 га — культурою s2, а p3*-ту частку 1 га — культурою s3.

Отже, засіявши поле культурами s1, s2, s3 у пропорції p1*, p2*, p3*, аграрне підприємство отримає за всіх погодних умов очікуваний валовий дохід, не менший числа V*. Зауважимо, що очікуваний валовий дохід з 1 га за j-го стану погоди буде принципово відмінним від фактичного, який є реалізацію випадкової величини А саме, за умови реалізації j-го стану погоди, підприємство, реалізувавши змішану стратегію sp*, одержить з імовірністю p1* фактичний валовий дохід fij; з імовірністю p2* — f2j; з імовірністю p3* — f3j. Проте відповідно до закону великих чисел фактичний валовий дохід за кілька років з великою ймовірністю дорівнюватиме очікуваному валового доходу V*.

Викладений тут результат легко узагальнити на випадок, коли висіваються т культур, а стани погоди деталізовано. Крім того, аналогічні моделі можна побудувати для випадку, коли підприємство має можливість змінювати не лише культури, які воно висіває, а й способи (технології) обробки поля.

Розв’яжемо числовий приклад для даних, наведених у табл. 1.2.

Отже, функціонал оцінювання (матриця виграшу першого гравця) має вигляд:

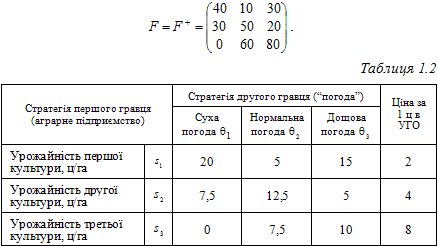
Оскільки α+ < β-, то гра не має сідлової точки, а тому оптимальна стратегія першого гравця змішана. Згідно з викладками, наведеними у додатку до розділу 1, пункт 1.8.1, для знаходження такої стратегії треба розв’язати задачу лінійного програмування:

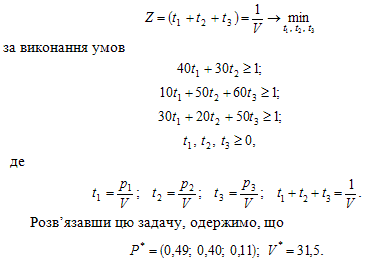
Тобто, за решти рівних умов, засіявши 49% поля першою культурою, 40% — другою, 11% — третьою культурою, аграрне підприємство отримає в середньому за низку років за різних погодних умов очікуваний максимальний валовий дохід не менший 31,5 ум. од. за рік.