Економічний ризик: ігрові моделі (2002)

Відповідно до класифікатора вважається, що в полі другої ІС (I2) суб’єкту ризику відомий закон розподілу ймовірності з точністю до невідомих параметрів. Якщо ці параметри складають вектор ω = (ω1;…; ωi), то отримуємо такий закон розподілу ймовірності станів економічного середовища:

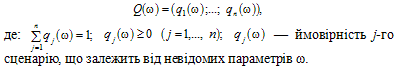
У [36, 104] розглядаються різні класи критеріїв прийняття рішень, ставиться задача параметричного синтезу оптимальних рішень, наводяться статистичні методи оцінювання значень параметрів, що складають вектор ω.

Коротко зупинимося на деяких основних підходах. Оскільки ω — вектор невідомих параметрів, то для нього також можна розглядати ІС Ilω(l = 1,…, 6), які називають ІС невідомих параметрів. У полі кожної з ІС щодо невідомих параметрів можна вибрати величини цих параметрів, що задовольняють, наприклад, принцип максимальної невизначеності Гіббса—Джейнса за певних обмежень. Після цього на основі знайденої оцінки ω вектора параметрів будується оцінка апріорного закону розподілу ймовірності Q = (q1;…; qn), а це, в свою чергу, дає можливість використання критеріїв прийняття рішень, що вивчалися в полі ІС I1.

Відповідно до класифікатора інформаційних ситуацій у випадку I1ω — відомий закон розподілу ймовірності вектора параметрів ω. А тому в якості точкової оцінки значень ймовірностей qj(j = 1,…, n) можна використати величини qj = M(qj(ω)).

Інший підхід базується на використанні параметричних критеріїв: Байєса, мінімальної дисперсії, модального тощо. Наприклад, згідно з параметричним критерієм Байєса оптимальна чиста стратегія sk0 вибирається відповідно до умови:

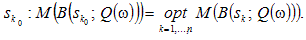
За наявності достатньої за обсягом вибірки інформації для оцінки невідомих параметрів можна скористатися статистичними методами. Наприклад, коли з точністю до невідомих параметрів відома функція щільності розподілу ймовірності станів економічного середовища, то невідомі параметри можна визначити на основі методу максимальної правдоподібності.