Економічний ризик: ігрові моделі (2002)
3.6.3. Критерій прийняття рішень у змішаних стратегіях у випадку протидії економічного середовища
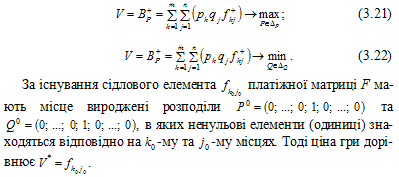
У випадку відсутності сідлового елемента платіжної матриці F = F+ рішення парної гри з нульовою сумою будемо відшукувати у змішаних стратегіях. Це означає, що «координатам» сідлових точок можна поставити у відповідність «стратегії», що знаходяться в «проміжках» між елементами дискретних множин S та Θ. Ці «стратегії» можна розглядати як «лінійні комбінації» елементів множин S та Θ з коефіцієнтами, що задають вектори P* = (p1*;…;pm*) та Q* = (q1*;…; qn*) відповідно.
За вибору першим гравцем (СПР) допустимої змішаної стратегії з розподілом P = (p1;…;pm) вектор:

Якщо від функціонала оцінювання F = F± перейти до матриці ризиків (невикористаних можливостей) Z = Z-, то оптимальну змішану стратегію СПР можна вибрати згідно з критерієм Севіджа. У цьому випадку має місце двокритеріальна задача виду (3.23)—(3.24), де замість fkj- використовуються елементи zkj- матриці Z-.
Зазначимо, що у випадку, коли виникає необхідність змінити інгредієнт функціонала оцінювання на протилежний, цього можна досягнути двома шляхами:
а) множенням на –1 елементів функціонала F, тобто переходом до функціонала F = -F = (-fkj : k = 1,…, n);
б) транспонуванням матриці F, тобто переходом до матриці FT = (fkj : j = 1,…, n; k = 1,… m).
Якщо отримані матриці (-F та FT) не мають сідлового елемента, то оптимальною змішаною стратегією P* СПР буде або оптимальна змішана стратегія першого гравця у грі, що визначається матрицею -F = (-fkj : k = 1,…, n; k = 1,… m), або оптимальна змішана стратегія другого гравця у грі, що визначається матрицею FT = (fkj : j = 1,…, n; k = 1,… m). При цьому точкова оцінка розподілу ймовірності Q* станів економічного середовища визначає або оптимальну змішану стратегію другого гравця (у грі, коли використовується -F = (-fkj : k – 1,…, m; j = 1,… n)), або оптимальну змішану стратегію першого гравця (у грі, коли використовується FT = (fkj : j = 1,…, n; k = 1,… m)). Крім того, сідловий елемент у матриці -F = (-fkj : k – 1,…, m; j = 1,… n) відсутній тоді і тільки тоді, коли відсутній сідловий елемент у матриці FT = (fkj : j = 1,…, n; k = 1,… m), і при цьому ціни ігор, що визначаються цими матрицями, рівні між собою за абсолютною величиною і мають протилежні знаки.