Економічний ризик: ігрові моделі (2002)
4.2. Формальна постановка багатокритеріальної задачі
Як і в попередніх розділах, для позначення основних елементів теоретико-ігрової моделі використовуватимемо ідентифікатори: S = (s1;…; sm) — множина альтернативних рішень СПР (чистих стратегій першого гравця); Θ = (Ө1;…; Өn) — множина станів економічного середовища (чистих стратегій другого гравця); F = (fkj : k = 1,… m; j = 1,… n) — функціонал оцінювання (платіжна матриця гри).
Мета, яка переслідується під час формування набору критеріїв оцінки якості стратегій, полягає в найбільш повному виділенні тих аспектів наслідків, які беруться до уваги під час порівняння різноманітних варіантів стратегій. При цьому набір критеріїв має задовольняти таким вимогам, як повнота, ненадмірність, операційність тощо.
Позначимо через e = (e1;…; eQ) множину локальних критеріїв, які вибрав СПР для порівняльного аналізу стратегій. Тоді кожній стратегії sk → S ставиться у відповідність вектор E(sk) = (e1(sk);…; eQ(sk)), який є кількісним відображенням спектру її якісних характеристик, що виділяються на основі цільового функціонала оцінювання F. Елемент eq(sk) = eq(F(sk)) = eq(fk1;…; fkn) вектора E(sk) являє собою реалізацію q-го критерію якості (кількісна оцінка q-ї якісної характеристики стратегії sk), F(sk) = (fk1;…; fkn) — вектор оцінювання, що відповідає стратегії sk.
Уведемо також до розгляду множину, складовими якої є вектори пріоритету об’єктів (інформаційних ситуацій, критеріїв якості стратегій тощо), що фігурують у процесі виокремлення оптимальних багатокритеріальних стратегій.
За вибору стратегії СПР доцільно оцінювати її з позиції незбіжних і, зокрема, суперечливих критеріїв. При цьому оптимальні значення цих критеріїв досягаються на різних елементах (стратегіях) з множини S. Це вказує на те, що вибір будь-якої стратегії з множини S, швидше за все, одночасно не забезпечить оптимум усім локальним критеріям. А тому перед СПР постає питання: згідно з яким принципом здійснювати вибір раціональної стратегії, «найкращої» з позиції усіх критеріїв якості. Вихід полягає в тому, щоб удатися до певної схеми компромісу критеріїв для досягнення поставленої цілі та дотримуватися його у виборі раціональної (компромісної) стратегії.
Отже, перед СПР постає задача вибору оптимальної (компромісної) стратегії sk0, що визначається двома умовами:
Стратегія має бути здійсненною, тобто sk0 → S;
Стратегія має бути найкращою у плані прийнятого в задачі принципу компромісу з урахуванням множини векторів пріоритету ∆.
Якщо через (E(sk); ∆) позначити сукупну інформацію, що характеризує різні аспекти якості стратегії sk та визначає важливість тієї чи іншої інформації для прийняття стратегій, то оптимальна (серед компромісних) стратегія має задовольняти умову:
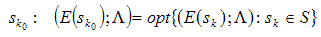
де символом opt позначено відповідний оператор оптимізації.
Оператор opt визначає принцип оптимальності, тобто принцип, що встановлює спосіб вибору найкращої стратегії серед множини усіх допустимих. Принцип оптимальності являє собою математичний вираз (математичну модель) прийнятого у задачі принципу компромісу. Конкретну сутність оператора opt необхідно вказувати для кожного випадку задачі прийняття рішення.