Менеджмент інвестиційної діяльності (2003)
4.2. Формування портфеля фінансових інвестицій та оцінювання його ризику і дохідності інституційним інвестором
Оцінюючи портфель та доцільність операцій з активами, що до нього входять, оперують такими показниками, як очікувана дохідність та ризик інвестиційного портфеля в цілому.
Очікувана дохідність портфеля інвестицій становить середньозважену величину очікуваних дохідностей кожного окремого активу, який входить до цього портфеля.
На відміну від очікуваної дохідності портфеля інвестицій стандартне відхилення портфеля інвестицій (Sp), яке характеризує, на скільки в середньому кожний варіант відрізняється від середньої величини, не є зваженою середньою стандартних відхилень окремих інвестиційних вкладень; залежність між ризиком портфеля та ризиком активів, що його формують, має більш складний характер.
Ризик для портфеля інвестицій вимірюється стандартним відхиленням розподілу доходів.
У багатоплановому випадку необхідно враховувати взаємозв'язок значень дохідності активів. Здійснюється це за допомогою показника коваріації (Cov) та коефіцієнта кореляції (R), які є базовими в аналізі інвестиційного портфеля.
Коваріація вимірює дві основні характеристики: варіацію доходів за акціями та тенденцію цих доходів змінюватися разам і одночасно. Додатна коваріація означає, що дохідність двох інвестицій має тенденцію змінюватися в одному напрямі за певний час. Від'ємна коваріація показує, що дохідність двох інвестицій має тенденцію змінюватися в різних напрямах за певний період.
Зазвичай величину коваріації досить складно інтерпретувати, оскільки це абсолютний статистичний показник; тому насамперед використовують коефіцієнт кореляції, який показує співвідношення двох змінних.
Коефіцієнт кореляції є загальнішим показником, оскільки стандартизує показник коваріації, що дає змогу проводити порівняння ступеня взаємозалежності доходів за різними групами інвестицій на загальній основі.
Коефіцієнт кореляції може змінюватися від -1 до +1: +1 — означає, що обидві змінні зростають і скорочуються абсолютно синхронно в одному напрямі (тобто доходи двох активів змінюються разом лінійно);
Коефіцієнт кореляції, який дорівнює нулю, свідчить, що обидві змінні не співвідносні (зміна однієї змінної не залежить від стану іншої).
Отже, коли портфель включає активи з додатною кореляцією, диверсифікація нітрохи не зменшує ризик; а при об'єднанні двох ризикових активів утворюється безризиковий портфель, якщо їх доходи змінюються в протилежних напрямах.
Якщо є декілька альтернативних інвестиційних портфелів, причому одні забезпечують вищий прибуток, а інші — нижче стандартне відхилення портфеля, то іноді доцільно розрахувати коефіцієнт варіації інвестиційного портфеля (CVp), який відображає відносну зміну величини ризику інвестування і розраховується як відношення стандартного відхилення інвестиційного портфеля S до величини його очікуваної дохідності:
CVP=^L. К
Як ілюстрація принципової залежності між ризиковістю активу, що розглядається ізольовано, та ризиковістю того самого активу, що аналізується з позиції портфельних інвестицій, розглянемо найпростіший приклад оцінювання ризику та формування портфеля з мінімально можливим ризиком.
Приклад 1
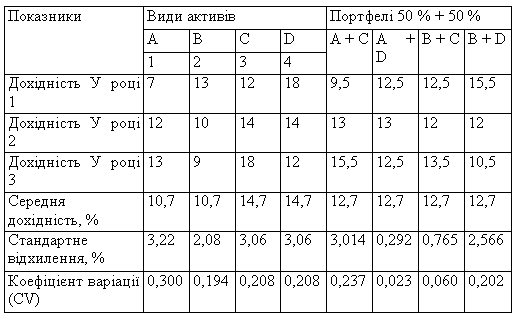
У табл. 4.3 наведено статистичні дані про дохідність фінансових інструментів А, В, С та D за останні три роки (див. стовпчики 1—4). Проаналізувати ризик цих інструментів, а також можливих портфелів, якщо менеджер може вибрати одну з трьох стратегій інвестування:
а) вибрати один із фінансових інструментів;
б) сформувати портфель, у якому 50 % буде становити актив А, а 50 % — актив С або D;
в) сформувати портфель, у якому 50 % буде становити актив В, а 50 % — актив С або D.
Розрахувати середню дохідність, стандартне відхилення та коефіцієнт варіації цих активів та можливих портфелів.
Розв'язок
Розраховані значення середньої дохідності, коефіцієнта варіації фінансових активів та можливих портфелів подано в табл. 4.З. Вихідні характеристики щодо портфельних інвестицій знаходять за формулою середньої арифметичної зваженої. Проілюструємо принцип розрахунку коефіцієнта варіації для активу А та можливого портфеля А + С

Отже, згідно з розрахованими значеннями стандартного відхилення та коефіцієнта варіації у міру зростання ризику фінансові інструменти упорядковуються таким чином:
актив В — найменш ризиковий;
актив С та D — більш ризиковані, ніж актив В;
актив А — найризиковіший.
З позиції портфельних інвестицій найменш ризиковий варіант, коли інвестор усі свої кошти вкладає в портфель, у якому 50 % становить актив А та 50 % — актив D (коефіцієнт варіації має найменше значення 0,023). Звернімо увагу, незважаючи на те, що найризиковішим є актив А, саме він входить до найменш ризикового портфеля.
Цікавим є також той факт, що два з можливих портфелі забезпечують менший рівень ризику, ніж будь-який з активів, що цей портфель формують.
Крім того, при формуванні портфелів з активами С або D (вони мають однакові значення середньої дохідності й відрізняються лише послідовністю значень дохідності за роками) необхідно надати перевагу включенню до них активу, що має тенденцію зміни дохідності, протилежну базовому активу.
Підкреслимо, що в цьому прикладі ми розглядали випадок, коли йшлося не про досягнення максимально можливої дохідності, а про формування найменш ризикового портфеля. Але зрозуміло, що досягнення високого рівня дохідності можливого інвестиційного портфеля, безумовно, є одним з головних завдань інвестиційного менеджера, тому виникає проблема оптимізації цільової комбінації ризику та дохідності.
Розглянемо інший приклад, який дасть нам можливість отримати краще уявлення про сутність оптимізації ризику та дохідності (активів) при формуванні інвестиційного портфеля.
Приклад 2
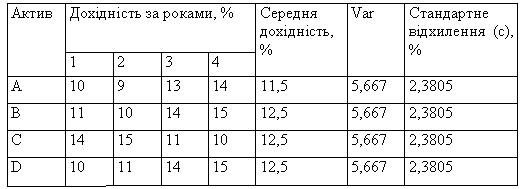
У табл. 4.4 наведено статистичні дані за останні чотири роки про дохідність фінансових активів А, В, С та D, що трактуються як однопродуктові портфелі. Розглядається доцільність комбінації цих активів за схемою 50 % + 50 %; тобто слід розглянути можливі варіанти формування портфелів із двох активів, причому 50 % портфеля має становити один актив, 50 % — інший. Розрахувати коефіцієнт кореляції та стандартне відхилення отриманих портфелів.
Розв'язок
Використання як ступеня ризику стандартного відхилення (див. табл. 4.4) дає можливість дійти висновку, що всі активи мають однакову ризиковість, і тому проблема полягає лише у формуванні найбільш дохідного портфеля, оскільки актив Л має найменшу середню дохідність порівняно з іншими активами. Але такий висновок є хибним.
Розглянемо можливі варіанти формування портфеля з двох активів та розрахуємо їхню середню дохідність, стандартне відхилення і коефіцієнт кореляції. Отримані значення показників наведено в табл. 4.5.
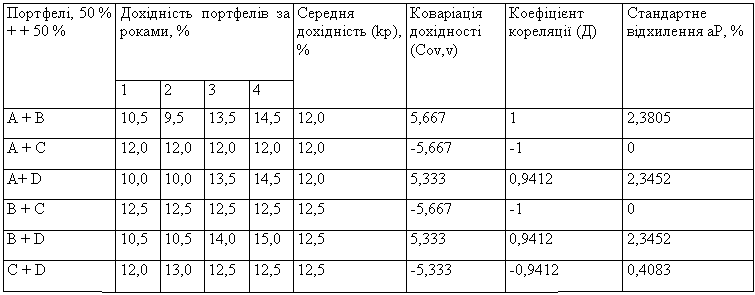
Проілюструємо принцип розрахунку необхідних показників на прикладі портфеля (С + D). Дохідність портфеля інвестицій обчислюється за формулою
Проаналізуємо отримані результати.
Портфелі (А + С) та (В + С) мають значення коефіцієнта кореляції —1 та стандартного відхилення 0; значення дохідності активів, що їх формують, пов'язані оберненою функціональною залежністю. Об'єднання таких активів приводить до усунення ризику, тобто отримання безризикової комбінації. Але внаслідок того, що портфель (В + С) забезпечує вищу середню дохідність, вибираючи можливий варіант інвестування слід надати перевагу саме йому.
Усі інші варіанти формування портфелів інвестицій займають проміжне положення між попередніми крайніми варіантами; дохідності їх активів мають кореляційну залежність (0 < R < 1) і, як наслідок, ризик можливих портфелів знижується (але суттєво — лише в комбінації (С + D)).
У даному прикладі ми розглянули ситуацію, коли в портфель об'єднували активи, що мають однаковий рівень ризику, і нам навіть вдалося отримати два абсолютно безризикових портфелі. Однак на практиці таке буває дуже рідко.
Аналіз реальних ситуацій на біржах провідних промислових країн показує, що, як правило, для більшості випадково відібраних груп акцій величина коефіцієнта кореляції становить від +0,5 до +0,7.
Як правило, при збільшенні кількості фінансових активів, що формують інвестиційний портфель, рівень ризику портфеля знижується. Таким чином, диверсифікація інвестиційної діяльності зменшує ризик за окремими групами акцій, але не може усунути його в цілому та повністю.
Отже, підсумуємо. При аналізі доцільності операцій з портфелем цінних паперів можуть вирішуватися три основні завдання:
досягнення максимально можливої дохідності;
отримання мінімально можливого ризику;
досягнення оптимально прийнятного для інвестора значення комбінації ризику та дохідності.
Об'єднання ризикових активів у портфель може приводити до зниження ризику порівняно з ризиком, властивим кожному з цих активів, взятих окремо. Однак результат залежить не лише від ризиковості активів, що об'єднуються, а й від характеру взаємозв'язку між їх дохідностями.
Якщо дохідність фінансового активу, який планується включити до портфеля, змінюється однонапрямлено з його дохідністю й описується кореляційною залежністю, то ризик нової комбінації може змінитися в будь-який бік порівняно з ризиком початкового портфеля.
При включенні до портфеля ризикового активу, дохідність якого змінюється однонапрямлено з дохідністю портфеля, але описується прямою функціональною залежністю, і значення варіації дохідності активів, що об'єднуються, та портфеля є однаковими — ризик нової комбінації залишається без змін.
Якщо ж до портфеля включається актив, дохідність якого змінюється різнонапрямлено з дохідністю портфеля, то ризик нової комбінації, як правило, зменшується.
Включення до портфеля безризикового активу зменшує дохідність портфеля, при цьому ризик портфеля зменшується прямо пропорційно до частки цього активу.
Наведені вище приклади дають змогу отримати уявлення про складність управління інвестиційним портфелем, не дарма послуги фахівців з управління портфельними інвестиціями оцінюються надзвичайно високо.
Операції з інвестиційним портфелем вимагають від інвестиційного менеджера вміння робити обґрунтовані прогнози щодо тенденцій дохідності на ринку цінних паперів у цілому і відносно активів, які планується включити до портфеля, та здійснювати складні й трудомісткі розрахунки в межах імітаційного аналізу і моделювання в умовах багатоваріантності можливих портфелів, оскільки йдеться про очікувані значення показників. Ці обчислення суттєво полегшує використання комп'ютера.
Одним із важливих понять у теорії портфельних інвестицій є поняття ефективного портфеля, під яким розуміється портфель, що забезпечує максимальну очікувану дохідність за деякого заданого ризику або мінімальний ризик за заданого рівня дохідності. Алгоритм визначення низки ефективних портфелів як складову теорії портфеля розробив Гаррі Марковіц. Марковіц показав, що зміна дохідності є визначальним виміром ризику портфеля. За певного рівня ризику інвестори надають перевагу більшим доходам порівняно з меншими. Так само за цього рівня очікуваних доходів інвестор надає перевагу меншому ризику порівняно з більшим.
За таких припущень окремі цінні папери або портфель вважаються ефективними, якщо ніякі інші цінні папери або портфель цінних паперів не дадуть вищої очікуваної дохідності за такого самого (або навіть меншого) рівня ризику. Зрозуміло, що ефективних портфелів може бути сформовано багато, тому вводиться поняття оптимального портфеля. Отже, інвестор будує низку кривих байдужості, тобто кривих, які відображають різноманітні комбінації дохідності та ризику. Вважається, що чим вище розташована крива, тим вищий і рівень задоволення вимог інвестора.
Далі будується набір ефективних портфелів, які відображаються ефективною межею чисельності портфелів (рис. 4.1).
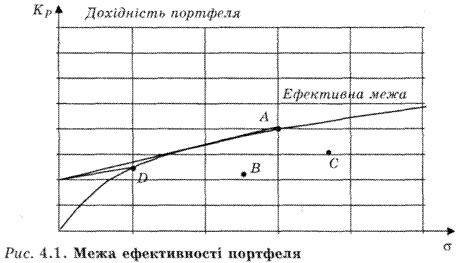
Якщо характеристики портфелів (точки А, В, С, D) розташовані на кривій ефективної межі, то портфелі є оптимально ефективними, або, інакше кажучи, найпривабливішими для інвестора з погляду співвідношення дохідності й ризику. Портфелі, характеристики яких розташовані під лінією, — менш ефективні (В та С).
Безпосередній вибір (тобто точка на ефективній межі) інвестора залежить від його ставлення до ризику. Чим більш схильний до ризику інвестор, тим більше його вибір оптимального портфеля буде зсунутим праворуч уздовж ефективної межі. Ця точка визначається перетином ефективної межі чисельності портфелів з кривою байдужості інвестора. Для того щоб швидко визначити портфель, який мінімізує ризик для кожного рівня доходу, необхідно використати математичний метод, що називається квадратичним програмуванням.
Отже, якщо інвестор приймає рішення в умовах визначеності, то визначити оптимальну комбінацію "ризик — дохідність" досить легко: потрібно шукати оптимальний портфель акцій для інвестора, не схильного до ризику, за допомогою математичного очікування та дисперсії. Розглянемо приклад формування інвестиційного фінансового портфеля із заданими характеристиками для більшої кількості активів та з імовірнісним розподілом можливих грошових потоків, що повертаються.
Приклад З
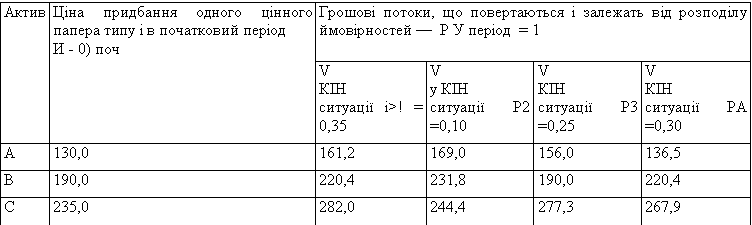
Визначити декілька можливих альтернативних інвестиційних портфелів із очікуваною дохідністю 16,0 % (що формуються з трьох активів А, В, С), якщо відомі початкова ціна придбання цінних паперів1 та грошові потоки, що повертаються (дивіденди плюс майбутня динаміка курсу), які неможливо точно спрогнозувати, є лише розподіли ймовірностей — Ps та плановий період інвестування ліквідних засобів обсягом 100 000 ум. гр. од. — t = 1. Вихідні дані для вибору інвестиційного портфеля подано в табл. 4.6.
Таблиця 4.7. Дохідність та ризик фінансових активів
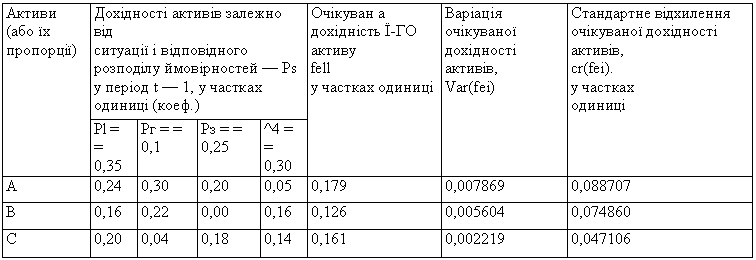
Отримані результати, подані у табл. 4.7, слід тлумачити таким чином: якщо настає ситуація Si, то, володіючи першим активом, ми досягаємо дохідності 24 %, володіючи другим активом — 16, третім — 20 % і т. д. Відповідно, очікувана дохідність активу А загалом становитиме 17,9 % , активу В — 12,6 % і т. д.
Розв'язання цільової функції лінійної оптимізаційної задачі для різних значень очікуваної дохідності інвестиційного портфеля дало можливість отримати наведені в табл. 4.8 структури портфелів, або співвідношення активів, що мінімізують ризик.
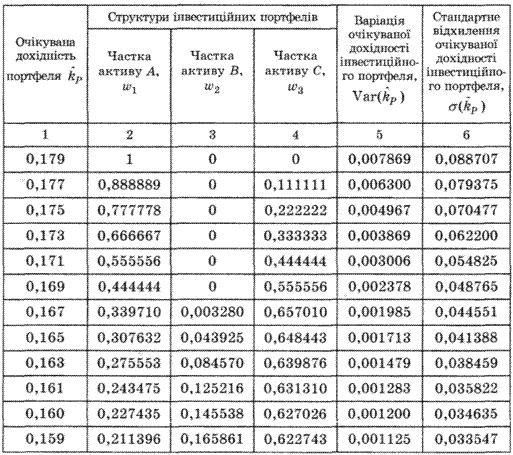
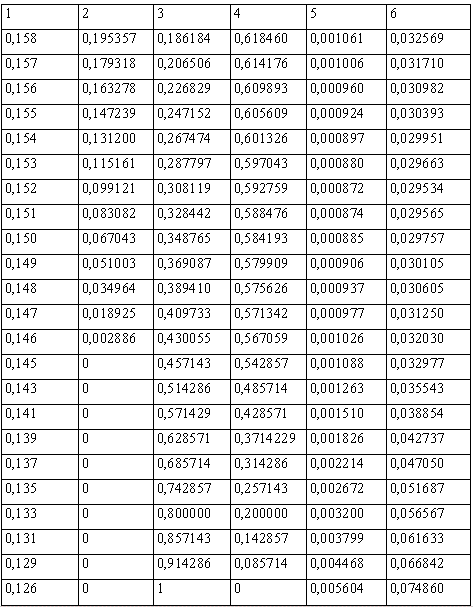
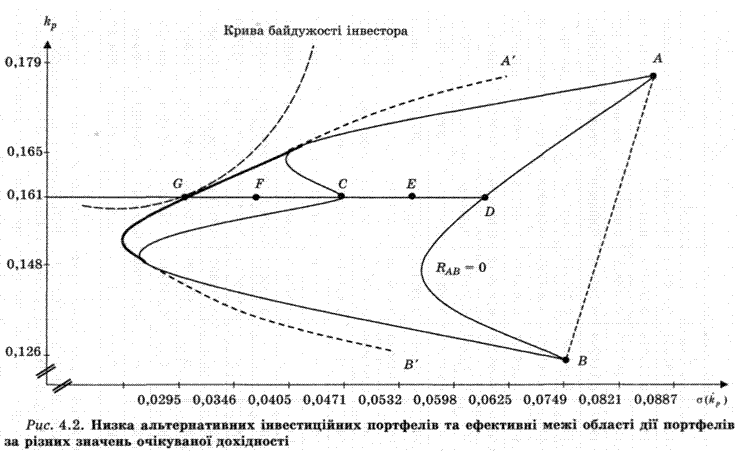
Найменш ризиковий інвестиційний портфель (o(kP) = - 0,029534) можна отримати за його очікуваної дохідності не вище 15,2 %. На основі даних таблиці 4.8 можна побудувати графік (рис. 4.2), на якому безпосередньо відображено ефективну межу області дії інвестиційного портфеля.
Зазначимо також, що якщо продаж без покриття можливий1, то для визначення оптимальної структури інвестиційного портфеля можна скористатися методом добутків Лагранжа. Отже, за відсутності у наведеній вище задачі оптимізації умови невід'ємності додаткові обмеження шляхом перетворень необхідно прирівняти до нуля, зважити їх, використовуючи добутки Лагранжа, і підставити у цільову функцію:
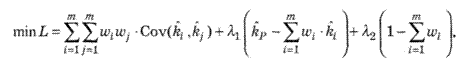
Прирівнявши похідні функції Лагранжа за wi (і = 1,..., т), за А,хта за А,2 до нуля, визначаємо частку активів, яка мінімізує ризик.
Виникає система лінійних рівнянь (т + 2) з (т + 2) невідомими, яка має, як правило, єдине розв'язання. В матричній формі запису система рівнянь виглядає так:
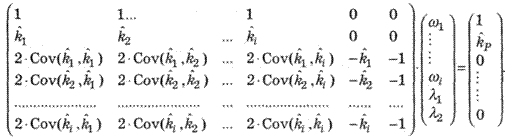
1 При продажу цінних паперів без покриття, або короткому продажу (short sales), інвестор спочатку дорого продає цінний папір, а потім дешево його купує. Продаж цінних паперів без покриття здійснюється шляхом запозичення цінних паперів або сертифікатів на них для використання у початковій угоді, а потім погашення позики такими самими цінними паперами, придбаними за наступною угодою. Це означає, що позичальник повинен віддати свій борг кредитору у формі передачі цінних паперів або сертифікатів на них, а не грошових засобів, а також, що позичальнику, як правило, не потрібно сплачувати ніяких відсотків за тимчасове користування запозиченими цінними паперами. Згідно з чинними у деяких країнах правилами, продаж цінних паперів без покриття не може здійснюватися в умовах падіння ринкового курсу цінних паперів, оскільки продавець, який не має власних цінних паперів, може загострити ситуацію, викликати паніку і відповідно отримати з цього значну вигоду. Тобто передбачається, що продаж цінних паперів без покриття має здійснюватися в умовах зростання реалізаційної ціни (за ціною, що перевищує ціну останньої угоди) або ж з нульовим приростом ціни (за ціною, що дорівнює останній угоді, але перевищує ціну останньої угоди за іншою ціною).

Для трьох цінних паперів отримаємо, відповідно:
Розв'язавши це рівняння відносно kP, ми отримаємо велику кількість можливих інвестиційних портфелів, які мінімізують ризик (відображені на рис. 4.2 відрізками А' та В') і не є ефективними, за умови, що продаж активів без їх покриття можливий. Результати розрахунків для деяких портфелів подано в табл. 4.9.
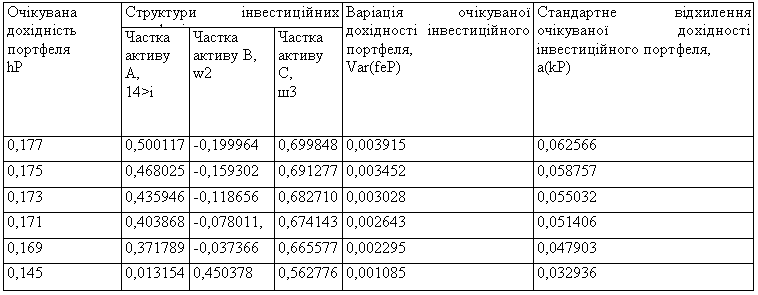
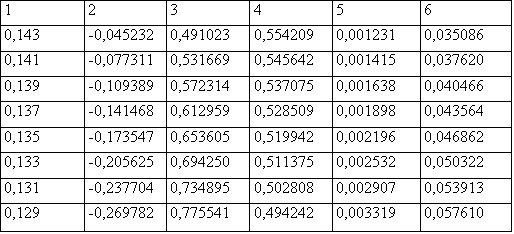
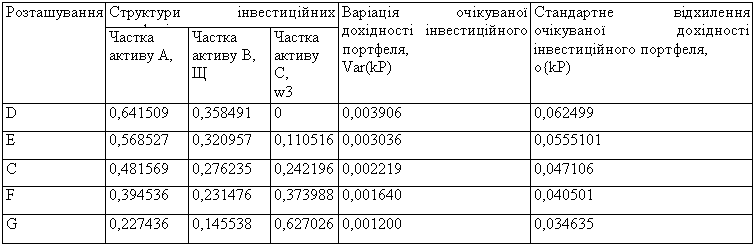
З метою ілюстрації практичної можливості отримання двох альтернативних варіантів вкладення коштів, що на рис. 4.2 характеризуються точкою С, пропонуємо до вашої уваги відповідні результати розрахунків структури портфелів та ризикованості запропонованих інвестиційних портфелів із очікуваною дохідністю 0,161 (табл. 4.11).
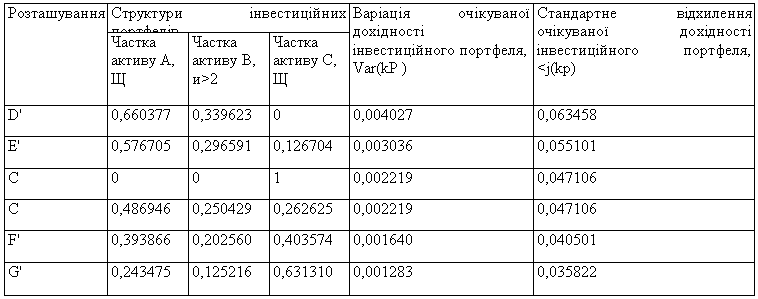
Отже, дані табл. 4.10 та рис. 4.2 доводять, що можна змінювати ризик інвестиційного портфеля, зберігаючи незмінною його очікувану дохідність, шляхом зміни його структури (при кількості активів більше двох). Крім того, можна досягти будь-якої точки співвідношення "ризик/дохідність", розташованої в межах фігури ABG (див. рис. 4.2), змінюючи відповідно структуру портфеля. Безпосередній вибір інвестора оптимального інвестиційного портфеля буде залежати від його схильності до ризику. Цей вибір відображається кривою байдужості інвестора, дотичною до кривої низки ефективних портфелів (або до кривої ефективної межі області дії портфеля).
Звідси, наявні у інвестора 100 000 ум. гр. од. ліквідних засобів, згідно з умовою завдання, можна рекомендувати вкласти таким чином:
22 750 ум. гр. од. в актив А (придбавши 175 шт. акцій);
14 440 ум. гр. од. в актив В (76 шт. акцій);
62 745 ум. гр. од. в актив С (267 шт. акцій).
Всього буде витрачено на придбання акцій 99 935 ум. гр. од.; залишок у касі — 65 ум. гр. од. Сумарна дохідність операції з урахуванням залишків у касі задовольняє всі поставлені у завданні умови.
Зазначимо, що в межах теорії вибору портфеля неможливий аналіз тих ризикових інвестицій, які не є цінними паперами, оскільки безпосереднє оцінювання коефіцієнта кореляції для інвестицій у придбання земельних ділянок, їх дослідження та розробку практично неможливе, тому що немає часових рядів. Крім того, якщо інвестор не орієнтується на принцип Бернуллі (орієнтація на математичне очікування та варіацію за умови, що функція корисності інвестора є квадратичною), а використовує принцип ц - а2 незалежно від того, чи нормальний розподіл дохідностей, альтернативні інвестиції^ іноді можна вважати однаково прибутковими (тобто kt = a(fe;)).