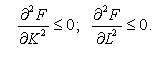Мікроекономічна теорія виробництва і витрат (2003)
1.2. Виробнича функція як технологічна модель системи «витрати—випуск»
У загальній формі виробнича функція має такий вигляд [21, с. 453]:
F(x, y, A)=0 (1.1)
де y — вектор випусків продукції;
х — вектор витрат ресурсів;
А — матриця параметрів.
Часто для виробничої функції застосовується такий вираз:
F(x1, x2, …, xi …, xn)=0
де змінні хі зі знаком «–» означають витрати, а зі знаком «+» — випуски.
В економічних дослідженнях звичайно фігурує виробнича функція у вигляді рівняння, в якому всі компоненти випуску (у натуральному або вартісному вимірі) об’єднано в одну скалярну величину (Y), а число (n) різнорідних виробничих ресурсів (хі) зведено до мінімуму, що допускає розрахунок параметрів виробничої функції на базі наявної інформації:
Якщо як незалежні змінні виступають обсяги витрат ресурсів (хі), то виробничу функцію заведено називати функцією випуску (виробництва), якщо ж незалежною змінною є розмір випуску (Y), то виробнича функція є функцією витрат.
У мікроекономічну теорію термін «виробнича функція» було введено в 1890 р. англійським математиком А. Беррі, який співробітничав з А. Маршаллом за підготовки математичного додатка до книги останнього «Принципи економічної науки». Однак спроби встановити залежність випуску від кількості застосовуваних ресурсів мали місце задовго до цього.
Виробнича функція багато в чому схожа на функцію корисності в теорії поводження споживача. Це пояснюється тим, що стосовно ресурсів підприємство є споживачем і виробнича функція характеризує саме цей аспект — виробництво як споживання.
Виробничі відносини на мікрорівні — це передусім технологічні відносини. Технологія являє собою сукупність прийомів і способів перетворення вихідних ресурсів на готову продукцію. Кожна технологія характеризується певною комбінацією факторів, необхідною для забезпечення випуску певного блага.
Функція виробництва показує максимально можливий випуск продукції (Q), що може бути досягнутий за розрахунковий період за кожної конкретної комбінації факторів виробництва:
Q = f(x1, x2, …, xi, … xn) (1.3)
де n — кількість видів споживаних ресурсів;
xi — обсяг застосування ресурсу i-го виду.
Вираз «максимально можливий випуск продукції» є принципово важливим. Ним підкреслюється, що ресурси не повинні витрачатися даремно. Будь-яка їх комбінація має використовуватися підприємством ефективно.
Виробничий процес, як правило, може бути організований по-різному, із застосуванням різних технологій. Виробнича функція описує множину технічно ефективних способів виробництва продукції. Спосіб виробництва вважається технічно ефективним, якщо не існує ніякого іншого способу, в який для виробництва заданого обсягу продукції витрачається менша кількість принаймні одного виду ресурсів без збільшення споживання всіх інших ресурсів. Якщо ж спосіб А припускає використання одних ресурсів у більшій, а інших — у меншій кількості, ніж спосіб Y, то обидва способи розглядаються як технічно ефективні й обидва включаються у виробничу функцію. Отже, спосіб виробництва є технічно ефективним, якщо вироблений обсяг продукції є максимально можливим у разі використання точно визначених обсягів ресурсів.
Після того, як підприємство визначило технічно ефективні способи виробництва, воно повинно вибрати з них один — економічно ефективний, тобто який забезпечує виробництво заданого обсягу продукції з мінімальними витратами чи за заданого розміру витрат забезпечує максимум випуску. Такий підхід дає змогу за збуту продукції збільшувати прибуток, обчислений як різниця між виторгом від реалізації продукції і витратами. Який з технічно здійсненних способів буде обрано і реалізовано, залежить від багатьох факторів, насамперед — від цін відповідних ресурсів.
Важливо мати на увазі, що виробнича функція відповідає деякому даному рівню технології. Якщо рівень технології змінюється внаслідок удосконалення матеріально-речовинних і особистісних факторів виробництва, то відповідно змінюється й виробнича функція.
«Пагорб виробництва» і варіації факторів. Виробнича функція може бути задана в табличний, аналітичний або графічний спосіб. Цінним інструментом вивчення виробничих функцій є їх геометрична інтерпретація.
За однієї незалежної та однієї залежної змінної [Y=f(x)] безупинна виробнича функція зображається лінією на площині з координатами у та х.
У мікроекономічній теорії традиційно застосовується двофакторна виробнича функція, в якій максимальний обсяг випуску продукції за період (Q) визначається комбінацією певної кількості використаних одиниць праці (L) і капіталу (K):
Q=f(L,K) (1.4)
Двофакторну функцію нескладно подати у графічному вигляді. Зауважимо, що графічні методи, поряд із своєю безперечною перевагою — наочністю, мають і суттєву ваду: вони обмежують дослідника тривимірним простором або ж двомірною площиною. Однак висновки, отримані для двофакторних моделей, як показують практика і дослідження багатьох учених, справедливі й для n-вимірних випадків.
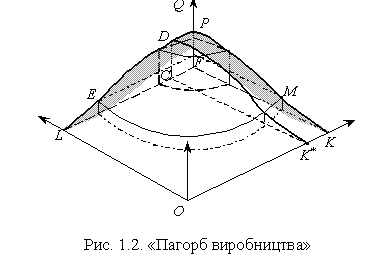
На рис. 1.2 у тривимірному просторі зображено двофакторну функцію виробництва: по горизонтальних осях відкладено кількісні значення факторів виробництва, по вертикальній — обсяг випуску за розглянутий період. Поверхня виробництва OKPL набула назву «поверхня випуску», або «пагорб випуску», або «пагорб виробництва», або «гора виробництва», а в німецькомовній літературі — «пагорб доходу», при цьому під доходом розуміється випуск у натуральному вимірі.
Поверхня виробництва описує всі можливі комбінації факторів виробництва і відповідні їм випуски.
Варіації факторів виробництва показують, як впливають на випуск продукції зміни комбінацій та обсягів застосування факторів.
Вертикальний розріз «пагорба» випуску площиною K*DC, рівнобіжної осі одного з факторів (на рис. 1.2 осі ОL), дає уявлення про часткову варіацію факторів виробництва, тобто динаміку випуску залежно від зміни витрат змінного фактора (L) за фіксованого значення другої координати (K*). Таку залежність заведено називати виробничою функцією короткострокового періоду, або короткостроковою функцією виробництва. Вона описується рівнянням
Q=f(x) (1.5)
де х — обсяг застосування змінного фактора в натуральному вимірі за період.
Саме це дало підставу називати її однофакторною, хоча слід розуміти, що кінцевий результат (випуск Q) формують обсяги застосування всіх залучених факторів — і постійних, і змінних.
Горизонтальний розріз «пагорба виробництва», наприклад, площиною ЕМF об’єднує варіанти виробництва, що характеризуються фіксованим випуском продукції за різних сполучень факторів, і на площині LOK такий розріз може бути поданий лінією рівного продукту.
У теорії виробництва криві рівного продукту (криві байдужності продукту) заведено називати ізоквантами (від грец. isos — рівний, однаковий та лат. quantum — скільки). Ізокванта — геометричне місце точок у просторі факторів виробництва, для яких характерний однаковий випуск. Отже, ізоквантна варіація показує, як можна комбінувати фактори виробництва для забезпечення визначеного обсягу випуску продукції.
Якщо зробити кілька горизонтальних розрізів пагорба виробництва, то можна одержати карту ізоквант підприємства (див. тему 3), на основі якої вивчається виробнича функція довгострокового періоду за пропорційної варіації факторів виробництва. Такий аналіз показує, як змінюється випуск у разі однакових пропорцій зміни обсягів застосування всіх факторів виробництва.
Вертикальний розріз «пагорба виробництва» двома площинами з фіксованими координатами K* і L* (одну з таких площин K*DС зображено на рис. 1.2, другу нескладно уявити — щоб не «затемнювати» рисунок її не наведено) дає уявлення про випуск у миттєвому періоді. Січна двох площин на «пагорбі виробництва» — це лінія випуску, а на площині факторів виробництва — точка, яка й визначає виробничу функцію миттєвого періоду.
Так, якщо для виробництва 100 од. продукції на місяць обрано технологію, для реалізації якої необхідно застосувати 300 годин роботи машин і 100 годин трудовитрат на місяць, а обсяги застосування факторів і потреба в продукції в силу зовнішніх і внутрішніх причин залишаються незмінними тривалий час, то максимальний випуск — 100 од. продукції на місяць — залишатиметься на цьому рівні, допоки принаймні одна з незалежних величин не зміниться (рис. 1.3).
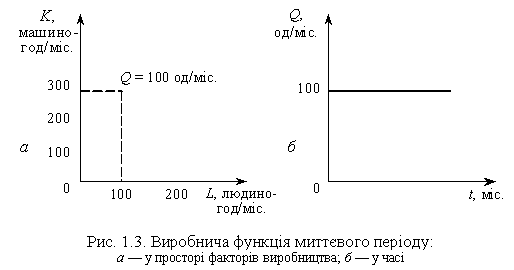
Такий миттєвий з економічного погляду період може тривати як завгодно довго. Наприклад, однопредметна потокова лінія з випуску певного типорозміру підшипників може працювати в заданому режимі з постійним тактом випуску кілька років, поки є стійкий попит на продукцію, що випускається. У миттєвому періоді фактори не варіюють за визначенням.
Існують й інші варіації факторів виробництва — повна, ізоклінна, непропорційна, які розглядатимуться в інших темах.
Кожний вид виробництва, як правило, описується різними виробничими функціями. Звідси випливає, що видів виробничих функцій так само багато, як і видів виробництв.
Не претендуючи на повноту систематизації, виділимо деякі види виробничих функцій, передусім ті, що використовуватимуться у подальшому викладі мікроекономічної теорії виробництва і витрат (табл. 1.1).

Наведемо стислу характеристику деяких видів виробничих функцій.
Виробничі функції довгострокового періоду описують взаємозв’язок між входом і виходом виробничої системи за умови, що обсяги застосування всіх факторів змінюються одночасно і, як правило, в одній пропорції, а функції надтривалого періоду враховують і вплив на результати виробництва революційних змін у технології.
В однофакторних виробничих функціях зміна результативного показника пов’язана зі зміною лише одного фактора (наприклад, вплив обсягів застосування праці на випуск продукції), у багатофакторних виявляється характер впливу на кінцевий результат комбінацій кількох виробничих факторів (трудовитрат, витрат матеріалів, часу роботи устаткування тощо).
У лімітаційних виробничих функціях між витратами факторів виробництва і кількістю продукції, що випускається, існують жорсткі технічні співвідношення, тобто певний виробничий результат (Q) може бути досягнутий у разі єдиної ефективної комбінації факторів. Найвідоміша функція цього виду — виробнича функція В. Леонтьева, що характеризується двома основними властивостями: лімітаційністю співвідношень між виробничими факторами та лінійною залежністю між витратами ресурсів і випуском, через що її часто називають лінійно-лімітаційною. Такі функції використовують для моделювання строго детермінованих виробничих процесів, у яких не припустимі відхилення від установлених норм використання ресурсів на одиницю продукції. Так, наприклад, на швейній фабриці для виготовлення однієї сукні потрібно 1,5 м2 тканини, одна застібка-блискавка, три гудзики і 0,5 машино-години роботи швейної машини.
У субституційних виробничих функціях немає жорсткого технічного взаємозв’язку між витратами факторів виробництва і випуском, тобто певна кількість продукції може бути вироблена за допомогою різних ефективних комбінацій факторів. Серед субституційних виробничих функцій вирізняють функції з повною (альтернативною, абсолютною) і частковою (периферійною, відносною) заміщеністю ресурсів. Наприклад, складання певних виробів можна виконати вручну за допомогою механізованого інструменту, а можна — за допомогою роботів, цілком виключивши ручну працю. Таке виробництво допускає альтернативну заміщеність факторів й описується відповідною виробничою функцією. Проте для багатьох виробництв існують як технічні, так і економічні межі заміщення факторів. Часткова заміщеність ресурсів зустрічається на практиці набагато частіше, ніж повна.
Однорідними, або гомогенними, називаються виробничі функції, що мають ті самі властивості на всіх інтервалах. У таких функціях результативний показник змінюється пропорційно значенню показників-факторів, тобто виконується умова
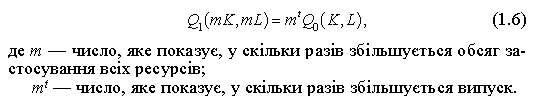
Показник t характеризує ступінь однорідності функції. Якщо
t = 1 — функція лінійно-однорідна;
t < 1 — функція дегресивно-однорідна;
t > 1 — функція прогресивно-однорідна.
Неоднорідними називаються виробничі функції, що мають різні властивості на різних інтервалах і потребують відповідного коригування за їх аналітичного і графічного подання.
Статичні виробничі функції не враховують час як фактор, який впливає на зміни основних характеристик досліджуваної системи, динамічні — враховують фактор часу.
Детерміновані виробничі функції моделюють виробничі закономірності без урахування непевності, тобто за стабільних очікувань можливих відхилень параметрів виробництва.
Стохастичні виробничі функції враховують імовірнісний характер процесу виробництва, його непевність, випадкові параметри, тобто так звані стохастичні перешкоди.
Існують й інші, досить повно описані в спеціальній літературі види виробничих функцій [8, 17 та ін.]. Виробничі функції можуть бути побудовані для окремого агрегату, дільниці, виду виробництва, підприємства, групи підприємств, підгалузі, галузі.
Адекватне відображення реальних співвідношень витрат ресурсів і випуску розпадається на дві взаємозалежні задачі:
специфікація виробничої функції, тобто виокремлення суттєвих факторів і визначення виду функції;
параметризація виробничої функції, тобто розрахунок чисельних значень її параметрів на основі систематизованих фактичних даних за допомогою регресійного і кореляційного аналізу.
І хоча виробничі функції є різними для різних видів виробництв, вони мають деякі загальні властивості, що характеризують особливості по’єднання факторів у виробничому процесі.
Випуск продукції без витрат ресурсів неможливий.
Цю властивість часто називають гіпотезою про абсолютну необхідність факторів виробництва, тобто
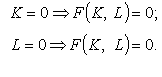
Ресурси передбачаються деякою мірою взаємозамінними, тобто певна кількість одного фактора може бути компенсована деякою кількістю іншого. Цю властивість називають гіпотезою про взаємозамінність факторів, тобто
F(K+∆K, L) = F (K, L + ∆L)
Виробнича функція передбачається неперервною і такою, що диференціюється. Цю властивість іноді називають гіпотезою про монотонність, що, звичайно, є деяким спрощенням реальності.
За збільшення витрат одного з ресурсів і фіксованого розміру інших ефективність застосування у виробництві додаткової одиниці змінного ресурсу знижується. Ця властивість називається умовою другого порядку, тобто