Мікроекономічна теорія виробництва і витрат (2003)
6.4. Короткострокові функції витрат за різних видів віддачі змінного фактора
За незмінних цін на ресурси і незмінної технології виробництва функція витрат є дзеркальним відбитком виробничої функції: якщо одна функція звернена опуклістю вгору, то зворотна до неї буде звернена опуклістю вниз і т. д. Як зазначалося в темі 2 (див. параграф 2.2), короткострокова функція виробництва з одним змінним фактором може описуватися різними типами рівнянь, кожне з яких відповідає тому або іншому характеру віддачі від уведення у виробництво додаткових одиниць цього фактора. Відповідно різними рівняннями описуються й короткострокові функції витрат (табл. 6.4).

Розглянемо математичне і графічне подання функцій витрат, а також їх економічну інтерпретацію за різної віддачі змінного фактора виробництва.
Функція витрат за постійної віддачі змінного фактора. Лінійні функції витрат характерні для виробництв із постійною віддачею змінного фактора. Іншими словами, лінійна функція виробництва визначає лінійність функції витрат (рис. 6.7).
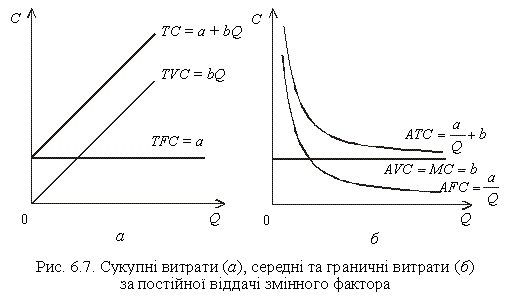
Якщо виробнича функція характеризується постійною віддачею змінного фактора, то загальний продукт (обсяг виробництва) зростає у тому самому ступені, що й застосування змінного фактора. За незмінної ціни ресурсу (а ми проводимо аналіз з урахуванням цього припущення) функції TVC і ТС — лінійні, тобто в міру збільшення обсягів випуску витрати збільшуються на постійну величину, як це показано на рис. 6.7, а.
Крива AFC постійно знижується зі зростанням випуску і має форму гіперболи. Її рівняння:
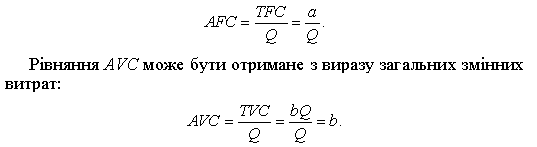
Це означає, що за постійної віддачі змінного фактора середні змінні витрати, так само як і середній продукт, незмінні.
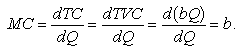
За постійної віддачі змінного ресурсу його граничний продукт МР також постійний, тобто AVC = MC = b, що й показано горизонтальною лінією на рис. 6.5, б, при цьому b — це нахил ліній TVC та TC.
Середні сукупні витрати АТС, за визначенням, дорівнють загальним витратам, поділеним на обсяг випуску. Отже, їхнє рівняння має вигляд:
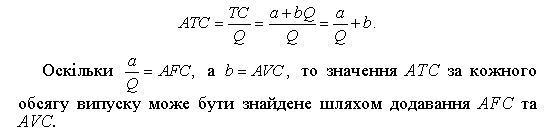
При цьому крива АТС має таку саму форму, що й крива AFC, і розміщена вище останньої на розмір AVC = b. Крива АТС знижується і наближається асимптотично до горизонтальної лінії AVC (див. рис. 6.7, б).
Наскільки реальним є розглянутий випадок? Емпіричні дослідження показують, що лінійні функції витрат мають багато підприємств різних галузей промисловості в досить широкому діапазоні змін обсягів виробництва. Однак з наближенням до межі фізичної виробничої потужності підприємства апроксимація поведінки витрат за допомогою лінійної функції не відповідає реаліям, оскільки не враховує дії закону спадної віддачі змінного фактора або, що те саме, закону неминучого зростання середніх (крім AFC) і граничних витрат.
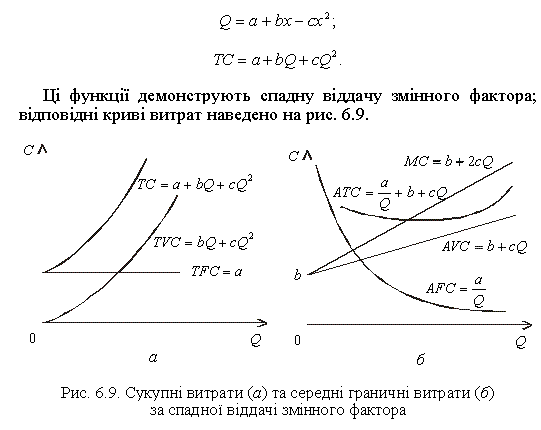
Функція витрат за зростаючої (спадної) віддачі змінного фактора. Як випливає з табл. 6.3, можливе існування двох типів квадратичних функцій витрат. Перший тип описується рівнянням для виробничої функції Q = a + bx + cx2, а для функції витрат — TC = a + bQ – cQ2. Такі функції демонструють зростаючу віддачу змінного фактора, їм відповідають криві витрат, наведені на рис. 6.8.

Форми кривих сукупних, середніх і граничних витрат прямо виводяться з форм кривих короткострокової виробничої функції. Вони, по суті, являють собою їхній дзеркальний відбиток. Аналітичні вирази для сукупних, середніх і граничних витрат виводяться аналогічно тому, як це було показано для функції витрат лінійного типу.
Можна зробити загальний висновок: якщо виробнича функція демонструє зростаючу віддачу від уведення додаткових одиниць змінного фактора, то в міру зростання обсягів випуску сукупні витрати (ТС і TVC) збільшуватимуться, але з уповільненням темпів приросту витрат, а середні та граничні витрати (AFC, AVC, ATC і MC) знижуватимуться: чим більше обсяг випуску, тим менше розміри всіх видів зазначених витрат. Іншими словами, чим більший обсяг випуску, тим нижчі витрати на одиницю продукції. Для підприємства — це найсприятливіший варіант. Однак, така віддача може спостерігатися тільки за освоєння нового виробництва, коли до незмінного розміру постійних факторів поступово додається змінний і його граничний продукт зростає. Після досягнення оптимальної пропорції факторів віддача стає або постійною, або спадною.
Другий тип квадратичної функції описується такими рівняннями для функцій виробництва і витрат:
Графоаналітичний аналіз усіх видів витрат та їх взаємозв’язків дає змогу зробити такі висновки: якщо функція виробництва характеризується спадною віддачею (зростання загального продукту уповільнюється в міру введення додаткових одиниць змінного фактора), то:
сукупні змінні витрати TVC і загальні витрати ТС збільшуються із зростанням обсягу виробництва;
середні сукупні витрати АТС знижуються, допоки зниження AFC «перекриває» збільшення AVC;
AТC зростають, якщо зростання AVC більше за зниження AFC.
Такий характер віддачі змінного фактора і такий вид функцій короткострокових витрат не є типовим для всього інтервалу можливих обсягів виробництва. Спадна віддача характеризує виробництво і витрати у разі майже повного залучення виробничої потужності. Після досягнення точки оптимальної пропорції постійного і змінного факторів усі види витрат, крім середніх постійних, зростають.
Кубічна функція витрат (зростаюча, а потім спадна віддача змінного фактора). У підручниках з мікроекономіки типовий характер зміни витрат на виробництво в короткостро- ковому періоді звичайно показується так, як це було наведено на рис. 6.5. Така функція витрат описується кубічним рівнянням
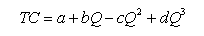
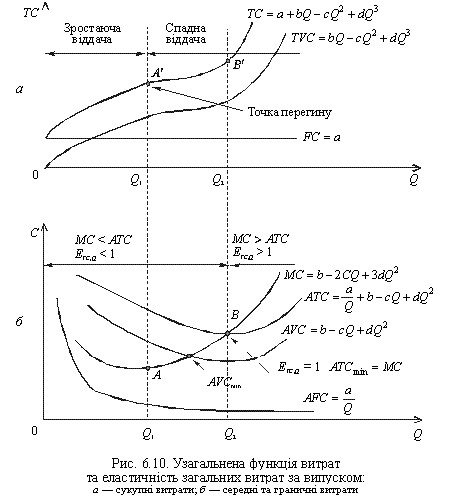
і добре ілюструє закон змінних пропорцій, тобто спочатку зростаючу, а потім спадну віддачу змінного фактора виробництва. Її часто називають узагальненою функцією короткострокових витрат (рис. 6.10).
Оскільки функція загальних витрат є кубічною, функції АТС, МС, AVC — квадратичні, мінімум МС (точка А на рис. 6.10, б) відповідає точці перегину кубічної функції загальних витрат (точка А на рис. 6.10, а). Точка перетинання кривих МС і АТС (точка В на рис. 6.10, б), у якій МС = АТСmin та ЕТС,Q = 1, відповідає оптимальному, тобто найбільш ефективному щодо витрат обсягу випуску (Qопт відповідає Q2).
Оскільки основні закономірності взаємозв’язків параметрів функцій витрат за зростаючої та спадної віддачі змінного ресурсу вже розглядалися (див. рис. 6.5, 6.9, табл. 6.3), докладніший коментар кубічної функції витрат допитливому читачеві пропонуємо зробити самостійно.
Як показує практика, в багатьох випадках кубічні функції витрат є чисто теоретичними узагальненнями. Всередині інтервалів зростання обсягів випуску від нуля до максимально можливого можуть існувати ділянки з різною віддачею, у тому числі постійною або майже постійною, можливі неодноразові зміни одного виду віддачі на інший і т. п. Щоб полегшити аналіз за таких ситуацій, у табл. 6.5 у зведеному вигляді наведено математичне подання функцій витрат різних типів і формули для розрахунку їхніх параметрів.

Результати емпіричних досліджень короткострокових функцій витрат. Економістами виконано безліч досліджень щодо поводження короткострокових витрат. Вони проводились як за окремими видами продукції, так і за агрегованими групами їх (сталь, сталевий прокат, меблі, трикотаж тощо), а також за галузями промисловості (машинобудування, електроенергетика, залізничний транспорт і т. ін.) [7, с. 237; 24, с. 431]. Виявилося, що для багатьох досліджуваних об’єктів зростаюча віддача змінного ресурсу спостерігається лише за невеликих обсягів випуску, потім має місце постійна віддача, при цьому максимальна ефективність — мінімум АТС — досягається у разі використання виробничих потужностей приблизно на 90 %, а далі МС, АVC й АТС різко збільшуються, тобто чітко виявляється спадна віддача. Останнє цілком зрозуміле: робота на межі виробничої потужності або ж «вихід» за цю межу пов’язані з організацією другої або третьої змін, продуктивність праці під час яких помітно нижча, ніж на першій зміні, з необхідністю оплати понаднормових робіт, із підвищенням інтенсивності використання устаткування, а отже, збільшенням числа поломок, аварій і т. п., що, у свою чергу, збільшує витрати виробництва.
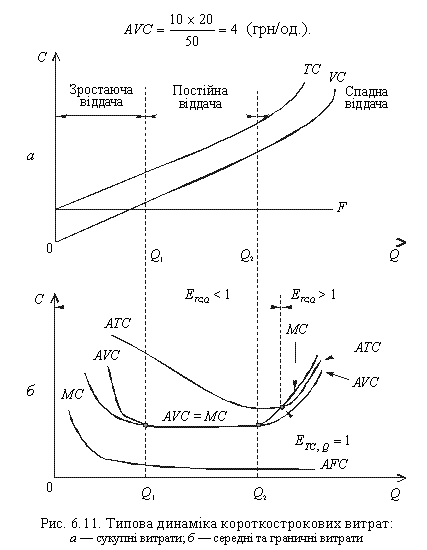
У такому разі криві граничних і середніх витрат також мають U-подібну форму, але з широким плоским дном (рис. 6.11).
Наявність широкого плоского дна, тобто блюдцеподібна форма кривих AVC і МС, дає змогу підприємству варіювати обсяг випуску без зміни середніх змінних витрат. Іноді діапазон обсягів випуску в інтервалі від Q1 і Q2 називають резервом потужності. Підприємство може заздалегідь готуватися до можливих коливань попиту і створити поле для маневру, розподіливши капітальне устаткування між самостійно функціонуючими ділянками, що випускають кінцеву продукцію. Щоразу, стикаючись зі збільшенням або зменшенням попиту на свою продукцію у межах від Q1 до Q2, підприємство може виключати (виводити) з виробництва дискретні ділянки, що дає змогу залишати незмінними середні змінні витрати. Припустимо, що виробник використовує 10 верстатів, які за зміну обслуговуються 10 робітниками і виробляють той самий продукт. Денна продуктивність 10 верстатів — 50 од., денна ставка одного робітника — 20 грн. Тоді середні змінні витрати становитимуть
Нехай денний попит знизився до 45 од. Це означає, що підприємство має зменшити число найманих робітників до 9 осіб і законсервувати один верстат, тобто одночасно змінити і постійний, і змінний фактори. «Закон» пропорцій, що змінюються, у такому разі не діє, середні змінні та граничні витрати не змінюються:
AVC=9*20/45 (грн/од.).
На закінчення наголосимо ще раз: знання виробником власних функцій короткострокових витрат має ключове значення для маневрування обсягами випуску і, за можливості, цінами з метою максимізації прибутку.
Ключові положення
Вид функції витрат залежить від характеру функції виробництва і цін на ресурси. Якщо ціни на ресурси і технологія в міру збільшення обсягів випуску залишаються незмінними, то функція витрат є дзеркальним відбитком функції виробництва.
Залежно від можливостей варіювання факторами виробництва розрізняють функції витрат миттєвого (фактори не варіюють), короткострокового (часткова варіація факторів) і тривалого (пропорційна і непропорційна варіації факторів) періодів.
У короткостроковому періоді зі зміною обсягу випуску продукції одні витрати залишаються постійними, а інші змінюються. Короткострокові загальні (сукупні) витрати на виробництво Q одиниць продукції дорівнюють сумі загальних постійних і загальних змінних витрат.
Короткострокові середні витрати — це витрати на одиницю продукції. Розрізняють три види короткострокових середніх витрат: середні сукупні, середні граничні, середні постійні витрати. Всі середні витрати визначаються розподіленням загальних витрат відповідного виду на обсяг випуску.
Короткострокові граничні витрати — це додаткові витрати на виробництво додаткової одиниці продукції; вони визначаються розподіленням приросту загальних витрат на приріст обсягу випуску.
Між кривими короткострокових середніх і граничних витрат існують певні взаємозв’язки: поки граничні витрати менші за середні змінні витрати, останні знижуватимуться; коли МС перевищать AVC, то AVC зростатимуть; аналогічно середні сукупні витрати знижуються, поки МС менші АТС. Отже, лінія граничних витрат перетинає лінії середніх змінних і середніх сукупних витрат у точках їхнього мінімуму.
Криві середніх змінних, середніх сукупних і граничних витрат мають дугоподібну форму, що пояснюється дією у короткостроковому періоді закону спадної віддачі змінного фактора, який часто трактують як закон незмінного зростання граничних і середніх (крім AFC) витрат.
Еластичність витрат за випуском характеризує ступінь реакції витрат на зміну обсягів випуску за інших рівних умов, кількісно вимірюється коефіцієнтом еластичності, що являє собою співвідношення відсоткових змін аналізованих показників. За необхідності можуть бути визначені коефіцієнти еластичності за випуском усіх видів витрат — загальних, середніх, граничних.
Якщо коефіцієнт еластичності загальних витрат за випуском ЕТС, Q < 1, то вони нееластичні за випуском, тобто відсоткове збільшення витрат менше, ніж відсоткове збільшення випуску, отже, має сенс уводити змінний фактор і нарощувати обсяги виробництва; якщо ЕТС, Q > 1, то загальні витрати зростають більшими темпами, ніж випуск, і подальше збільшення обсягів застосування змінного фактора економічно невигідне. Обсяг випуску, за якого ЕТС, Q = 1, а сукупні середні витрати мінімальні, є точкою технологічного оптимуму короткострокового періоду. Саме в ній досягається найкраще сполучення рівнів використання постійних і змінних ресурсів.
Короткострокова функція витрат з одним увідним змінним фактором може описуватися різними типами рівнянь, кожне з яких відповідає тому або іншому характеру віддачі від уведення у виробництво додаткових одиниць змінного фактора. Постійна віддача описується лінійним рівнянням; віддача, що зростає, — квадратичним І виду; спадна віддача — квадратичним ІІ виду; змінна віддача (зростаюча, потім спадна) — кубічним рівнянням.
Однак результати емпіричних досліджень показують, що зростаюча віддача має місце лише у період освоєння випуску нової продукції, потім спостерігається досить тривалий період постійної віддачі і лише з наближенням до 90—100-відсоткового рівня використання виробничих потужностей виявляється спадна віддача змінного ресурсу. Така «блюдцеподібна» форма кривих середніх і граничних витрат дає змогу підприємству маневрувати випуском без зміни середніх змінних витрат.
Знання виробником власних функцій короткострокових витрат має ключове значення для ефективного маневрування в ринковому просторі. Порівняння середніх сукупних і середніх змінних витрат із ринковою ціною дає змогу судити про прибутковість або збитковість продукції. Порівняння граничних витрат, що показують, як дорого обійдеться підприємству випуск ще однієї додаткової одиниці продукції, з граничним прибутком від її продажу уможливлює визначення підприємством оптимальних обсягів випуску, що максимізують прибуток або мінімізують збитки. Крім того, дослідження зміни середніх та, особливо, граничних витрат має велике значення за освоєння нової продукції. Такий аналіз дає змогу раціонально організувати процес виведення нового товару на ринок з мінімально можливими витратами, а отже, і з підвищеним рівнем конкурентоспроможності.