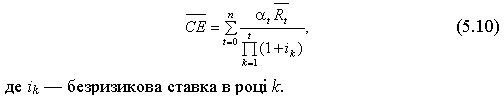Кількісні методи в управлінні інвестиціями (2000)

В основі методу еквівалента певності (МЕП) лежить ідея, що фінансовий менеджер може передбачити рівні ризику отримання грошових надходжень від інвестицій у період існування проекту.

Беручи до уваги обмеження економічного прогнозування, буде слушним передбачити, що оцінки грошових потоків більш ранніх періодів точніші, ніж оцінки останніх років періоду.

Коли використовується метод ЕП, сподівана вартість розподілу імовірностей грошових надходжень проекту в період t множиться на коефіцієнт еквівалента певності (КЕП), який ми визначимо як . Даний коефіцієнт перетворює ризиковані сподівані грошові надходження проекту в безризикові чи безпечні грошові надходження.

КЕП має значення від 0 до 1. Чим вище КЕП, тим більша частина сподіваних грошових надходжень у період t вважається менеджером безризикованою.

Оскільки в методі ЕП за допомогою КЕП ризик компенсується цілковито за визначенням, то дисконтування безризикових грошових потоків доцільно здійснювати за безризиковою ставкою, а не за вартістю капіталу фірми.

Безризикова ставка прибутковості звичайно асоціюється зі ставками прибутковості державних цінних паперів, оскільки вони є короткостроковими і мають гарантований прибуток і обов’язкову виплату номіналу при погашенні. Безризикові ставки прибутковості є точним відображенням вартості грошей у часі.

Коли обговорювався метод ЧТВ, в ролі ставки дисконту грошових потоків використовувалася вартість капіталу фірми, яка відображала її нормальний рівень ризику і включала в себе безризикову ставку і ставку, необхідну для компенсації комерційного і фінансового ризиків. З допомогою КЕП компенсується фінансовий і комерційний ризик отримання відповідних грошових надходжень, які потім дисконтуються за безризиковою ставкою дисконту.

Модель ЕП визначається таким рівнянням:

Зазначимо, що підхід ЧТВ об’єднує разом процес дисконтування та управління ризиком, у той час як метод ЕП дезагрегує процес управління ризиком за допомогою КЕП і дисконтування вартості грошей у часі за безризиковою ставкою.

Для використання методу ЕП важливо мати процедуру визначення КЕП. Спочатку здійснюється ретроспективний вибір інвестиційних проектів за їх основними видами — інвестиційні проекти із заміни основних фондів, з розширення виробничих потужностей, досліджень і розробок, які в свою чергу розділяються на кілька категорій. Потім усередині кожної категорії на щорічній основі визначаються рівні ризику і прибутковості. Результатом даного аналізу є узагальнені розподіли ймовірностей грошових надходжень проектів, на основі яких визначаються коефіцієнти варіації. КЕП для кожного року і для кожної категорії проекту задається згідно з інтервалами значень коефіцієнтів варіації.

● Приклад 2. МЕП

Компанія XYZ розробила значення КЕП і використовує їх в оцінці нового інвестиційного проекту з такими сподіваними прибутками і стандартними відхиленнями протягом 4-х років:

Якщо ми передбачаємо, що безризикова ставка не зберігається постійною в період існування проекту, рівняння (5.9) може бути представлене в загальнішому вигляді (рівняння 5.10):