Кількісні методи в управлінні інвестиціями (2000)

Будь-яка випадкова величина, представлена розподілом імовірностей, має математичне сподівання та стандартне відхилення. Річні грошові надходження інвестиційних проектів — це також випадкові величини з відповідними розподілами ймовірностей, що мають відповідні математичні сподівання і стандартні відхилення.

Випишемо загальну формулу визначення дисперсії суми трьох випадкових величин X, Y і Z, кожна з яких помножена на константу (a, b і с ) відповідно:

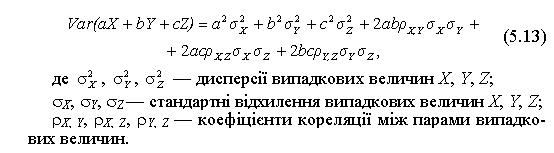
Зазначимо, що перші три складові дисперсії суми трьох випадкових величин показують внесок дисперсій трьох випадкових величин, а останні три — внесок коваріацій між усіма парами випадкових величин.

Тепер припустимо, що випадкові змінні X, Y і Z — це грошові надходження інвестиційних проектів відповідно в роки 1, 2 і 3; аналогічно константи a, b і с — процентний фактор теперішньої вартості відповідно в роки 1, 2 і 3, що відображає вартість грошей у часі при даній безризиковій ставці, тобто:

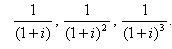
Тоді, виходячи з цього, можна зробити два припущення про взаємодію грошових надходжень проекту в період його існування — (1) потоки щорічних грошових надходжень проекту є незалежними і (2) потоки щорічних грошових надходжень абсолютно залежні.

Розглянемо кожен випадок.

Випадок 1. Незалежні потоки щорічних грошових надходжень проекту

Незалежність грошових потоків означає, що між ними не може існувати будь-якої систематичної залежності, а тільки випадкова залежність.

Подібний вид залежності грошових потоків може зустрічатися на ринках з високою конкуренцією, де відсутні торгові марки, реклама тощо, де екзогенні ринкові сили формують ринковий попит. Тому мінливість грошових потоків у період існування проекту знижуватиметься завдяки відмові від грошових потоків, вищих або нижчих від сподіваних.

За даного припущення всі парні коефіцієнти кореляції між грошовими потоками дорівнюватимуть 0. Тому останні три доданки в формулі дисперсії суми трьох випадкових величин теж дорівнюватимуть 0. Формула (5.13) набуває такого вигляду:

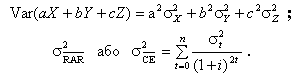
Випадок 2. Абсолютно залежні потоки щорічних грошових надходжень проекту

За даного припущення вважається, що при відповідному значенні грошового потоку першого року всі подальші грошові надходження є зумовленими. Такий взаємозв’язок між грошовими потоками може існувати на ринках з монополістичною конкуренцією, переповнених торговими марками, могутньою рекламою, та ще й з обмеженим входженням на ринок тощо. Мінливість тут буде більшою, ніж у випадку 1. Це пов’язано з тенденцією зростання ризику, викликаною позитивною кореляцією, яка виникає через нестачу протидіючих дисперсій, вищих або нижчих від середніх у період існування проекту.

У цьому разі передбачається, що всі парні коефіцієнти кореляції між щорічними грошовими надходженнями проекту дорівнюють + 1.0. Тоді рівняння (5.13) перетворюється у таке:

Виходячи зі своїх кривих корисності та оцінок міри взаємодії потоків грошових надходжень, фірма залишає чи відкидає інвестиційний проект.

● Приклад 4. Оцінювання двох інвестиційних проектів з використанням методу еквівалента певності

Нехай проект А має первинні інвестиції $200, 3-річний період існування і наступні розподіли грошових надходжень за періодами:

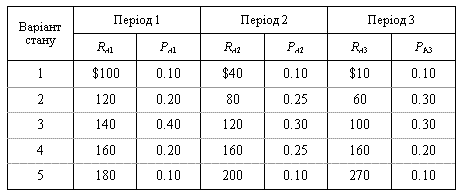
Фірма також оцінює проект D з первинними інвестиціями $300, 3-річним періодом існування і наступними розподілами грошових надходжень за періодами:

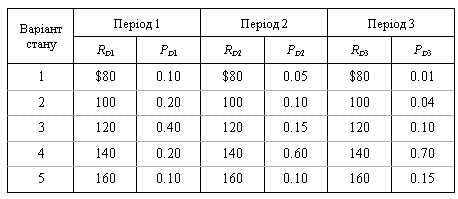
Безризикова ставка — 6%.

Фірма передбачає такі коефіцієнти еквівалента певності для двох проектів:

Розв’язання.

Для визначення значення Z використовується таблиця площі cтандартної нормальної кривої.

7.1. Незалежні грошові надходження.

Розраховуємо значення Z за формулою: