Менеджмент виробничих витрат у сільському господарстві (1998)
10.3.3. Побудова чисельної економіко-математичної моделі та розв’язання задачі

До основних констант моделі слід віднести загальну посівну площу (9,5 га), річний фонд робочого часу фермера та членів його сім’ї (5000 людино-год), їхній місячний фонд робочого часу (417 людино-год), річний еталонний виробіток трактора МТЗ80 (1800 у. ет. га), суму готівки, яку фермер може використовувати в процесі виробництва протягом року (23 тис. грн.), наявність коштів з урахуванням короткострокових банківських позик для придбання оборотних коштів (500 тис. грн.). Маючи необхідні техніко-економічні коефіцієнти та константи, побудуємо чисельну економіко-математичну модель, яка має такий вигляд.
1. Обмеження за використанням ріллі:
Х1 + Х2 + Х3 + Х4 + Х5 + Х6 + Х7 Х8 <= 0.
Це обмеження означає, що загальна площа посіву не може перевищувати 9,5 га.
2. Обмеження дотримання сівозмін:
Х1 + Х2 Х3 Х4 Х5 Х6 Х7 <= 0,
яке означає, що площа посіву під картоплею, помідорами, огірками та іншими овочами не може перевищувати площу посіву зернових культур.
3. Обмеження за питомою вагою помідорів у структурі посівних площ:
Оскільки помідори є найбільш трудомісткою культурою, вводиться умова, що в структурі посівних площ вони не можуть перевищувати певної питомої ваги. У нашому прикладі це 5 %.
4. Обмеження за азотними добривами:
45Х1 + 40Х2 + 120Х3 + 90Х4 + 120Х5 + 60Х6 + 70Х7 Х9 = 0.
5. Обмеження за фосфорними добривами:
55Х1 + 40Х2 + 90Х3 + 120Х4 + 120Х5 + 90Х6 + 80Х7 Х10 = 0.
6. Обмеження за калійними добривами:
45Х1 + 40Х2 + 150Х3 + 90Х4 + 120Х5 + 90Х6 + 100Х7 Х11 = 0.
7. Обмеження за обсягом механізованих робіт:
4Х1 + 3,8Х2 + 3,9Х3 + 28Х4 + 3,9Х5 + 35Х6 + 30Х7 Х12 <= 0
при Х12 = 1800.
Це обмеження означає, що загальний обсяг механізованих робіт у фермерському господарстві не може перевищувати річну продуктивність трактора МТЗ80, яка становить 1800 га умовної еталонної оранки.
8. Обмеження за використанням робочого часу:
15Х1 + 9,4Х2 + 175Х3 + 1040Х4 + 320Х5 + 765Х6 + 300Х7 Х13 Х14 = 0
при Х13 = 5000, де 5000 людино-год річний фонд робочого часу фермера та членів його сім’ї.
2,1Х1 + 2,8Х2 + 70Х3 + 312Х4 + 16,5Х5 + 38,3Х6 + 60Х7 Х15 Х31 = 0
при Х15 = 160; Х31 = 417, Х14 Х15 >= 0, де 417 людино-год середньомісячний фонд робочого часу фермера та членів його сім’ї; 160 людино-год можливі затрати праці залучених працівників у піковий період сільськогосподарських робіт.
10. Обмеження за оплатою праці залучених працівників:
10Х14 Х16 = 0.
11. Обмеження за витратами на садивний матеріал:
1840Х1 + 1980Х2 + 92000Х3 + 28000Х4 + 2000Х5 + 7700Х6 + 25000Х7 Х17 = 0.
12. Обмеження за вартістю мінеральних добрив:
11Х9 + 9Х10 + 6Х11 Х18 = 0,
де коефіцієнти показують вартість 1 кг діючої речовини відповідного виду добрив.
13. Обмеження за витратами палива:
113,1Х1 + 101Х2 + 221Х3 + 394,7Х4 + 429,4Х5 + 400,2Х6 + 350Х7 Х19 = 0.
14. Обмеження за вартістю палива:
50Х19 Х20 = 0.
15. Обмеження за обсягами транспортних робіт:
20Х1 + 15Х2 + 170Х3 + 80Х4 + 160Х5 + 90Х6 + 110Х7 Х21 = 0.
16. Обмеження за вартістю транспортних робіт:
10Х20 Х22 = 0,
де коефіцієнт показує вартість 1 ткм.
17. Обмеження за витратами на капітальний ремонт трактора та сільськогосподарських машин:
18. Обмеження за витратами на поточний ремонт трактора та сільськогосподарських машин:
80Х1 + 76Х2 + 78Х3 + 550Х4 + 75Х5 + 700Х6 + 600Х7 Х24 = 0.
19. Обмеження за витратами на технічне обслуговування й заміну гуми:
100Х1 + 152Х2 + 156Х3 + 1120Х4 + 157Х5 + 1350Х6 + 180Х7 Х25 = 0.
20. Обмеження за іншими виробничими витратами:
105Х1 + 110Х2 + 1250Х + 1140Х4 + 310Х5 + 1115Х6 + 280Х7 Х26 = 0.
21. Обмеження за грошовими надходженнями:
14400Х1 + 14400Х2 + 368000Х3 + 1280000Х4 +
+ 297000Х5 + 1350000Х6 + 180000Х7 Х27 = 0.
22. Обмеження за використанням готівки:
Х16 Х28 <= 23000.
23. Обмеження за наявними коштами для придбання оборотних фондів:
Х16 + Х17 + Х18 + Х20 + Х22 + Х23 + Х24 + Х25 + Х26 Х29 = 0
при Х29 <= 500000.
24. Обмеження за валовим прибутком:
Х27 Х16 + Х17 + Х18 + Х20 + Х22 + Х23 + Х24 + Х25 + Х26 = 0.
Цільова функція моделі має такий вигляд:
Х10 + Х17 + Х18 + Х20 + Х22 + Х23 + Х24 + Х25 + Х26 min
У табл. 10.12 наведено результати розв’язання задачі з використанням ПЕОМ. Задача розв’язувалася за чотирма варіантами залежно від змін окремих обмежень моделі. Так, варіант 2 передбачав відміну обмеження за дотриманням сівозмін, варіант 3 відміну обмеження за мінімумом коштів для придбання оборотних фондів, варіант 4 відміну обох зазначених обмежень.
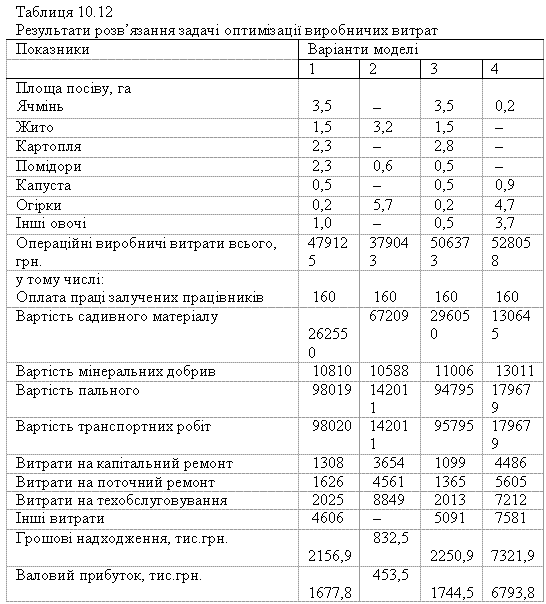
Аналізуючи розв’язання задачі за різними варіантами моделі, можна зробити висновок про доцільність здійснення тих чи інших заходів (попередньо зімітувавши їх у моделі) за умов оптимізації виробничих витрат і максимізації рівня ефективності господарювання. У нашому прикладі доцільним є третій варіант моделі, оскільки він забезпечує дотримання майже всіх вимог базової моделі. Другий та четвертий варіанти моделі є недоцільними через порушення сівозмін й високу інтенсивність використання наявних трудових ресурсів. Пояснюється це тим, що в умовах селянських господарств овочі вирощуються в основному вручну, а тому з такою концентрацією виробництва трудомісткої продукції фермерське господарство не зможе справитися.
Результатом розв’язання задачі є також отримання значень двоїстих оцінок обмежень, які показують, наскільки зміниться сума операційних виробничих витрат при зміні змінної на одиницю її розмірності.
За результатами розв’язання задачі, використовуючи значення двоїстих оцінок, можна відповісти на ряд важливих запитань, що стосуються функціонування фермерського господарства. До таких запитань слід віднести.
1. Чи доцільно додатково орендувати землю та яка гранична орендна плата за 1 га землі може бути виплачена орендодавцеві?
2. Чи доцільно залучати додаткову робочу силу для роботи в господарстві та яку максимальну оплату праці 1 людино-год може допустити фермер?
3. Якою може бути гранична ціна (з позиції мінімального рівня прибутковості господарювання) за одиницю купованих матеріальних ресурсів (добрив, палива, насіння тощо)?
4. Як зміниться прибуток за рахунок зміни потужності трактора, що використовується в господарстві?
5. Як зміниться прибуток, якщо замість оранки з повним обертом пласта землі застосувати безполицевий обробіток ґрунту?
Усі ці та подібні до них запитання мають безпосередній зв’язок з виробничими витратами. До переваг оптимізації виробничих витрат за допомогою комп’ютера слід віднести й те, що розроблена модель може бути використана в кожному наступному виробничому циклі з метою ефективнішого комбінування виробничих ресурсів в умовах зміни окремих технікоекономічних коефіцієнтів (цін на промислову й сільськогосподарську продукцію, системи оподаткування та ін.).
Отже, оптимізація виробничих витрат за своїм економічним змістом є логічним завершенням математичної інтерпретації функції виробничих витрат.