Бізнес-планування (2006)

Розглянемо на такому прикладі ще одну важливу проблему — порівняння взаємовиключних проектів з різними термінами життя.

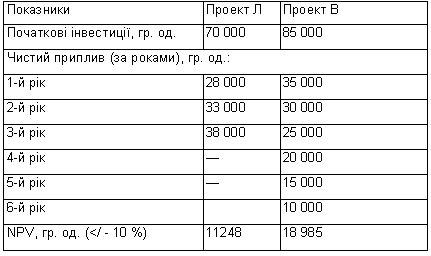
Проведений розрахунок NPV кожного проекту може привести до початкового висновку про необхідність із двох взаємо-виключних проектів прийняти проект В. Насамперед зазначимо, що термін "продуктивності" проекту В на три роки більший і саме ця обставина привела до перевищення його чистої приведеної цінності над NPV проекту А в нашому розрахунку. Але ми не можемо не враховувати чинника альтернативності при ухваленні рішення: альтернативна вартість прийняття проекту В дорівнює вартості того чистого прибутку, що міг би принести заперечений нами проект А, який функціонує в рівних із проектом В умовах, тобто протягом 6 років.

На практиці найчастіше так і виходить: проводять порівняння в умовах рівності термінів життя взаємовиключних проектів (при цьому звичайно використовують найменше загальне кратне їхніх термінів життя) продовжуючи короткий проект до терміна життя довгого і навпаки. У нашому випадку добудуємо проект А його трирічним продовженням. Якими при цьому взяти щорічні величини чистих грошових надходжень?

Розглянемо результати розрахунку NPV проекту Л залежно від трьох можливих варіантів (варіант 1 — повне повторення вже наявного потоку з четвертого року; варіант 2 — щорічні значення взяті на рівні середніх за перші три роки; варіант З — щорічні значення взяті на рівні останнього третього року).

Способи розрахунків за варіантами подано в умовних грошових одиницях.

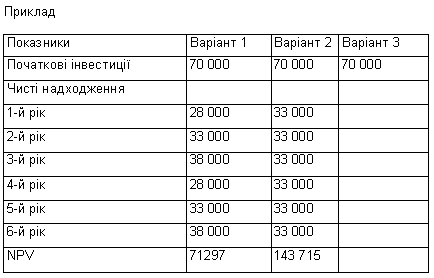
Як видно з розрахунку, навіть мінімальне значення NPV проекту А більше за NPV проекту В, що змінює наше початкове рішення і схиляє шальку терезів на користь проекту А. Але немає повної впевненості в об'єктивності цього рішення, тому що воно базувалося на прийнятій нами гіпотезі про ту чи іншу щорічну величину чистого надходження, а це, як ми бачимо з наведених даних, дає значний розкид розрахункових значень NPV проекту. Крім того, значне продовження терміну життя проекту (у нашому випадку в два рази) не може насправді не привести до збільшення початкових інвестицій, від чого ми абстрагувалися в цьому найпростішому прикладі, але зобов'язані враховувати на практиці.

Таким чином, розглянутий прийом, звичайно, має право на існування, але не забезпечує повної об'єктивності прийнятого рішення. Вільним від зазначеної хиби є спосіб ухвалення рішення на базі розрахунку ANPV (Annualized Net Present Value)2, ануїтованої чистої приведеної цінності як частки від розподілу NPV певного проекту на значення ануїтету за кількістю років проекту і взятої для розрахунку NPV ставки відсотка.

У цьому прикладі для проекту A ANPV =11 248 : 2,487 = = 4523; для проекту В ANPV = 18 986 : 4,355= 4359.

Звідси можна зробити висновок, що прийняти необхідно проект А, для якого значення ANPV вище.

У такий спосіб вирішуються деякі можливі конфлікти між ранжуванням взаемовиключних проектів за різноманітними критеріями ефективності та мінімізуються можливі помилки при прийнятті інвестиційних рішень. Проте в ході оцінювання ефективності інвестицій необхідно пам'ятати про можливість виникнення помилок і не покладатися на упорядкування проектів лише за одним критерієм, тим більше, що кожний із критеріїв підкреслює якийсь особливий аспект стану проекту. Разом вони дають найбільш повну картину ефективності прийняття інвестиційних рішень.

"Project Expert 6" дає можливість розраховувати модифіковані показники ефективності проектів за такою схемою.

Обчислюється майбутня вартість проекту (Terminal value) — вартість надходжень, отриманих від реалізації проекту, яка віднесена до кінця проекту з використанням норми рентабельності реінвестицій. Норма рентабельності реінвестицій у такому випадку означає прибуток, що може бути отриманий при реінвестуванні надходжень від проекту.