Менеджмент інвестиційної діяльності (2003)

У процесі використання методу лінійного програмування для визначення оптимального плану розподілу інвестиційних ресурсів слід дотримуватися двох основних вимог:

при визначенні оптимального портфеля інвестицій необхідно вибирати одиничні інвестиційні цілі;

цільова функція та обмежувальні рівняння мають перебувати у лінійній залежності.

У випадку, коли постійні показники, що використовуються у математичних моделях, не є точно визначеними величинам, доцільно використовувати їх очікувані значення, розраховані за допомогою прогнозованих ймовірностей виникнення тієї чи іншої події.

Розглянемо специфічний приклад використання методу лінійного програмування в процесі оптимізації портфеля інвестицій підприємства.

Приклад 4

Інвестиційному менеджеру доручено розмістити 150 000 ум. гр. од. капіталу так, щоб отримати максимум річних відсотків із вкладених коштів. Його вибір обмежений чотирма можливими об'єктами інвестицій: А, В, С, D. Об'єкт А дає змогу отримувати 7 % річних; об'єкт В — 10; об'єкт С — 14; об'єкт D — 12 % річних.

Кожний з розглядуваних проектів може бути подрібнений, тобто є можливість його часткового фінансування. Причому, щоб не піддавати капітал ризику, менеджерові рекомендовано не менше 40 % всіх інвестицій спрямувати в об'єкти А та В; щоб забезпечити ліквідність — не менше 25 % капіталу вкласти в об'єкт D; в об'єкт С у зв'язку з особливостями державного регулювання можна вкласти не більше 20 %, а в об'єкт А передбачається за раніше укладеними договорами вкласти не менше 15 %. Необхідно знайти таку комбінацію вкладень, яка максимізувала б дохідність інвестиційного портфеля за названих вище обмежень.

Розв'язок

Сформулюємо умову завдання у термінах лінійного програмування. Нехай X. є загальною величиною інвестицій в і-й об'єкт, тоді дохідність всього портфеля є середньозваженою сумою його складових. Звідси необхідно максимізувати цю суму.

Задача формулюється так:

максимізувати

F = 0,07 * Xj + ОД • Х2 + 0,14 • Х3 + 0,12 * Х4 за умови, що

Х1+Х2+Х3+Х4< 150 000; Х1 + Х2 > 0,4 (Хх + Х2 + Х3 + Х4); Х3<0,2 (Хі+Хз+Хз+Х^; Х4 > 0,25 (Х1 + Х2 + Х3 + Х4); Х^О.15 (Хх + Х2 + Х3 + Х4), деХ1,Х2,Х3,Х4>0.

Перетворивши зазначені рівняння до прийнятного вигляду, отримаємо таку систему рівнянь:

0,07 • Xt + 0,1 • Х2 + 0,14 • Х3 + 0,12 • Х4 = max; Xt + Х2 + Х3 + Х4 <150 000; 0,6-Х1+0,б-Х2-0,4-Х3-0,4-Х4 > 0; -0,2ХГ0,2'Х2+0,8-Х3-0,2'Х4 < 0; -0,25 • X, - 0,25 • Х2 - 0,25 Х3 + 0,75 • Х4 > 0; +0,85 X, -0,15-X,-0,15 Х3-0,15 Х4 > 0,

Зазначимо, що цю систему обмежень цільової функції можна подати і в іншому вигляді, якщо через X виразити частку інвестицій в і-й об'єкт.

Є багато комп'ютерних програм, які розв'язують подібні задачі. Наприклад, можна скористатися фінансовими функціями програми калькуляції електронних таблиць EXEL 7.0. Отже, не заглиблюючись у питання лінійного програмування, подамо розв'язок:

Xj = 22 500 ум. гр. од. (або 15 % загального обсягу здійснених інвестицій);

Х2 = 37 500 ум. гр. од. (25 % всіх інвестицій); Х3 = ЗО 000 ум. гр. од. (20 % інвестицій); Х4 = 60 000 ум. гр. од. (або 40 % здійснених інвестицій); Дохідність цього портфеля становитиме 11,15 % (або 16 725 ум. гр. од. на рік).

Завдання для самостійного розв'язання

1. Підприємство розглядає доцільність включення до портфеля реальних інвестицій декількох запропонованих до реалізації проектів. За позитивних результатів оцінювання NPV та незначного ризику втрати капіталу ці проекти вважаються однаковою мірою інвестиційно привабливими. Реалізація проектів не може бути відкладена на майбутні періоди, але може передбачати часткову участь інвестора. На теперішній момент підприємство може спрямувати на реальне інвестування 1 млн ум. гр. од.; середньозважена вартість капіталу, сформованого за рахунок власних джерел, становить ЗО % .

На основі вихідних даних запропонованих до реалізації проектів (див. табл.) необхідно сформувати оптимальний портфель реальних інвестицій поточного періоду.

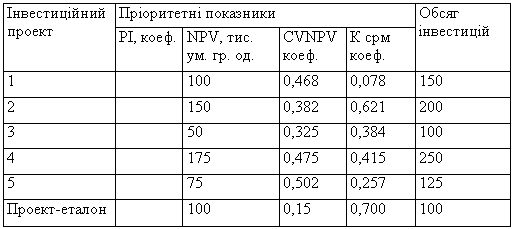
2. Підприємство планує спрямувати на реальне інвестування 500 000 ум. гр. од. Причому передбачається, що в процесі здійснення інвестиційної діяльності буде досягнуто максимізації чистих грошових потоків проектів, загальної ефективності використання капіталу, кількості створених робочих місць на підприємстві, а також мінімізації проектних ризиків. Необхідно сформувати оптимальний інвестиційний портфель, якщо керівництво розглядає як інвестиційно привабливі низку проектів і вважає за доцільне взяти участь у їх реалізації у міру можливостей. Вихідні дані для розв'язання проблеми оптимізації портфеля реальних інвестицій подано в таблиці.

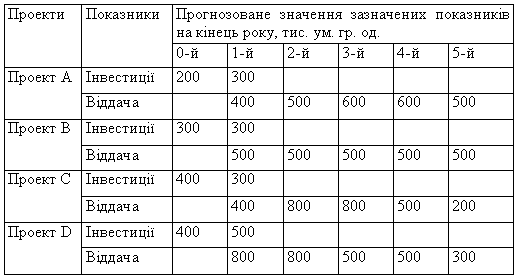
3. Підприємство планує оптимально розподілити за роками інвестиції між декількома проектами, щоб максимізувати їх сумарний NPV. На початковий період (t = 0) підприємство має вільні фінансові ресурси обсягом 200 000 ум. гр. од. власних коштів, а також 150 000 ум. гр. од. запозичених засобів, які передбачається використати на інвестування. Протягом наступних трьох років прогнозується щорічно отримувати з внутрішніх джерел фінансування по 250 000 ум. гр. од., а у другому році реалізації інвестиційної програми заплановано взяти короткотерміновий банківський кредит сумою 100 000 ум. гр. од. для збільшення обігових засобів.

До розгляду запропоновано п'ять інвестиційних проектів, що мають трирічний термін реалізації і характеризуються приблизно однаковою мірою ризикованості. Проекти у разі необхідності можуть бути прийняті до реалізації на умовах часткового фінансування. Значення результативного показника NPV та обсяги необхідних інвестиційних витрат за проектами узагальнено подано в таблиці.

Необхідно скласти цільову функцію та обмежувальні рівняння лінійного програмування для визначення оптимального плану розміщення інвестицій підприємства.