Кількісні методи в управлінні інвестиціями (2000)

МОКА передбачає лінійне співвідношення між прибутковістю проекту (ЦП) і ринковим чинником. Випадкова величина Qj передбачається незалежною від ринкового чинника і незалежною від випадкових чинників, що впливають на інші проекти (ЦП). Внаслідок цих припущень, які загалом не є вірними, певна частина реальної мінливості Е(Rj) втрачається. Тож портфелі, що створюються з допомогою МОКА, є менш ефективними порівняно з портфелями, що створюються за допомогою коваріаційного методу.

Лінія ринку капіталу

Оптимальний портфель окремого інвестора лежить у точці дотику його карти байдужості й ефективної множини портфелів, загальної для всіх інвесторів. Та оскільки карти байдужості в кожного інвестора різні, то й оптимальні портфелі в них також можуть бути різні.

Агреговані переваги індивідуальних інвесторів відбиваються лінією ринку капіталу (рис. 7.2).

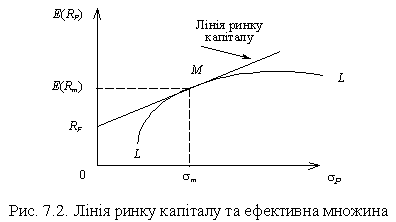
Для того, щоб ринок капіталу перебував у рівновазі, портфель М повинен містити кожен ризиковий актив у точній пропорції з тими частками, які кожний актив займає в загальній вартості всіх ризикових активів на ринку. Загальна мета всіх інвесторів — досягти максимальної диверсифікації, тому вони прагнуть включити до свого портфеля цінні папери всіх видів, які тільки є. Наприклад, якщо частка вартості звичайних акцій компанії А в загальному вартісному обсязі всіх акцій на ринку складає 0.65%, то акції А мають складати 0.65% тієї частини інвестиційного портфеля, що складається з акцій. Інвестор фактично купує «частинку ринку капіталу».

Портфель у точці М, що включає вартість кожного ризикового ринкового активу, зважену за її часткою в загальній ринковій вартості всіх ризикових активів, називається ринковим портфелем.

Нехай RF — це процент, який можна отримати на державних цінних паперах (ДЦП). Назвемо такі ДЦП «безризиковими активами» (default-free asset).Розглянемо можливі портфелі, які можна скласти, комбінуючи ринковий портфель з такими ДЦП. Нехай інвестор вклав частку α своїх активів до ринкового портфеля і частку (1 – α) — в ДЦП. Нехай α > 0. Тоді сподівана прибутковість інвестиційного портфеля E(RP) описується рівнянням:

Точка RF на ЛРК описує прибутковість портфелів, що складаються з безризикових активів. Рухаючись вище по ЛРК, інвестор зосереджує наявні кошти в портфелі з дедалі більшою часткою ризикових активів. Зростаюча схильність до придбання ризикованіших активів збільшує портфельну прибутковість E(RP). У точці М інвестор усі наявні в нього кошти вкладає в ризиковані активи. Між точками RF і M інвестор знаходиться в позиції кредитора, тобто вкладає кошти в обмін на активи й одночасно частину коштів віддає під фіксований процент RF. За точкою М інвестор починає сам позичати кошти за безризиковою ставкою та інвестувати їх за ринковою ставкою. Позика збільшує сподіваний прибуток, але ризик портфеля теж зростає.

Якщо вибрати точку на кордоні ефективності LL, відмінну від М, то при тому ж ступені ризику можна досягти значнішої сподіваної прибутковості шляхом комбінацій вкладень до ринкового портфеля і портфеля безризикових активів, знаходячись при цьому на ЛРК (на відрізку RFM або правіше точки М).

ЛРК використовується лише для особливої категорії портфелів, тобто для тих, що складаються з комбінації ринкового портфеля та безризикових активів.

Лінія ринку цінних паперів

Лінія ринку капіталу пов’язана зі сподіваною прибутковістю портфеля. Лінія ринку цінних паперів (ЛРЦП) показує необхідну прибутковість кожного ЦП в залежності від ризику (рис. 7.3).

Кожен ЦП у ринковому портфелі ризикових активів оцінюється таким чином, що його сподівана прибутковість обчислюється як:

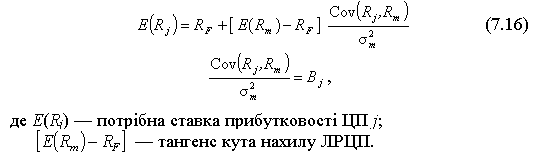
Потрібна прибутковість ЦП залежить від таких чотирьох чинників:

1. Безризикової ставки;

2. Сподіваної прибутковості ринкового портфеля;

3. Дисперсії ринкового портфеля;

4. Коваріації прибутковості ЦП з прибутковістю ринкового портфеля.

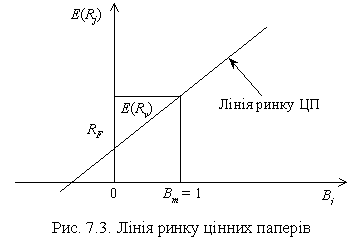
ЛРЦП відрізняється від ЛРК тим, що:

(1) для окремого ЦП мірою ризику є коваріація, а не стандартне відхилення. Це пояснюється тим, що ризик окремого ЦП залежить від його вкладу в ризик портфеля, де він знаходиться;

(2) ризик ринкового портфеля вимірюється його дисперсією, а не стандартним відхиленням.

Вплив інфляції

Безризикова ставка RF фактично вираховується на основі ставки за казначейськими цінними паперами. Цю ставку ще називають номінальною ставкою. Вона складається з двох елементів: реальної безінфляційної ставки прибутку — R* і премії за інфляцію І, яка дорівнює передбачуваному рівневі інфляції. Отже:

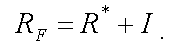
Якщо рівень інфляції змінюється, то це веде до паралельного зсуву ЛРЦП. Згідно з МОКА збільшення RF веде до відповідного збільшення прибутку з усіх ризикових активів. Премія за інфляцію є невід’ємною частиною потрібної ставки прибутку як ризикових, так і безризикових активів.

На рис. 7.4 наочно показаний зсув ЛРЦП під впливом зростання рівня інфляції. Нехай реальна безризикова ставка прибутку R* = 3%, а первісний рівень інфляції І = 3%. Тоді RF1 = R* + I = 3% + 3% = 6%. Якщо рівень інфляції зростає на ΔІ = 2%, тоді RF2 = R* + (I + ΔІ) = 3% + (3% + 2%) = 3% + 5% = = 8%. Лінія ЛРЦП1 переміщується вгору в положення ЛРЦП2. Зростають на 2% і потрібні ставки прибутку з усіх цінних паперів. Наприклад, за середніми ЦП ставка прибутку зросла з 11% до 13%.

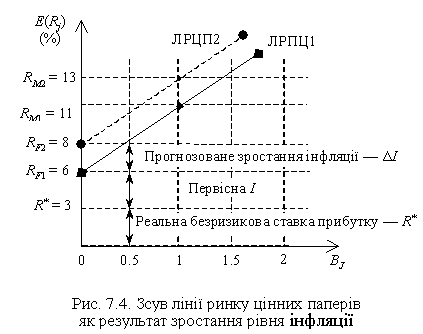
Вплив неприймання ризику

Нахил ЛРЦП відображає ступінь неприймання ризику інвестором. Чим більший нахил лінії, тим вищий ступінь неприймання ризику. Інвестор, індиферентний щодо ризику, матиме горизонтальну ЛРЦП, бо для інвестора премія за ризик відсутня. При підвищенні неприймання ризику зростає і премія за ризик, і відповідно ступінь нахилу ЛРЦП.

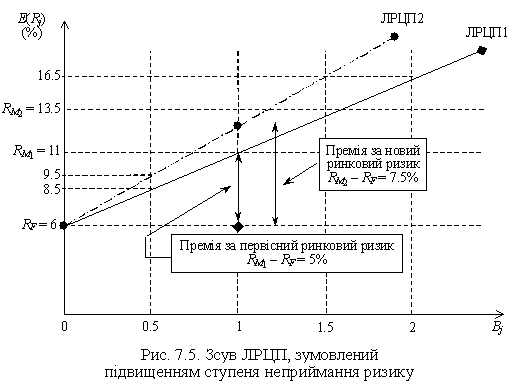
Рис. 7.5 ілюструє підвищення ступеня неприймання ризику. Премія за ринковий ризик зросла з 5% до 7.5% при BJ = 1. Прибутковість ринку ЦП зросла також з 11% до 13.5%. Прибуток за іншими ЦП також зростає, причому ефект даного зсуву вельми впливає на більш ризикові ЦП. Скажімо, прибуток за ЦП з BJ = 0.5 зростає лише на 1% — з 8.5% до 9.5%, у той час як прибуток ЦП з BJ = 1.5 зростає на 3%, з 13.5% до 16.5%.

Використання МОКА для оцінки інвестиційних проектів покажемо на прикладі.

● Приклад 2. Використання МОКА для аналізу інвестиційних проектів

Нехай задаються певні чотири стани економіки Si, i =1, 2, 3, 4, з імовірностями настання pi, i = 1, 2, 3, 4. Крім того, задані ринкова норма прибутковості проекту — Rm та прогнози норм прибутковості чотирьох проектів A, B, C, D — відповідно RAі, RBі, RCі та RDі. Безризикова ставка RF = 0.08. Здійсніть вибір найкращого проекту.

Розв’язання.

Складемо таку таблицю: