Економічний ризик: ігрові моделі (2002)
3.1.1. Критерій Байєса та його модифікації

Під час використання критеріїв (3.2) чи (3.3) необхідно звернути увагу на таке застереження: рішення (чисту стратегію) можна вважати оптимальним лише в тому випадку, коли у СПР є підстави для того, щоб усі елементи функціонала оцінювання F віднести до зони допустимого ризику. Якщо ж це не так, то використання критерію Байєса є некоректним, він не враховує варіацію. У цьому випадку для прийняття рішень ризик доцільно розглянути як векторну величину, компонентами якої є такі показники, як величина допустимого, критичного та катастрофічного ризиків тощо (див. пункт 2.3.6).
Дослідження показують, що навіть у випадку сприятливої (щодо СПР) ситуації рішення, прийняте лише на основі критерію Байєса, не є адекватним, тобто воно не враховує всі аспекти реальної ситуації. А тому оцінки, отримані згідно з цим критерієм, часто використовуються як складові складніших критеріїв, що враховують розкид значень функціонала оцінювання на множині станів економічного середовища (це розглядатиметься далі). До останніх належить критерій, наведений у [33]:
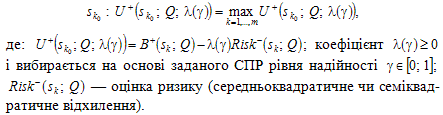
Якщо від функціонала оцінювання F = F+ перейти до матриці невикористаних можливостей (матриці ризиків) Z = Z-, то вибір оптимального рішення (стратегії) можна здійснювати аналогічно. При цьому слід скористатися критерієм (3.3), де
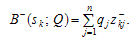
Але, як це показано у додатку до розділу 3 (пункт 3.9.2, теорема 3.3), оптимальна чиста стратегія sk0,вибір якої ґрунтується на критерії Байєса з використанням матриці невикористаних можливостей Z-, одночасно є оптимальною згідно з цим критерієм, якщо використовувати функціонал оцінювання F.
Цей факт ще раз підтверджує раніше зроблений висновок щодо неврахування ризику за використання критерію Байєса.
Наведемо кілька прикладів.


Приклад 3.2. Підприємство випускає певну продукцію партіями фіксованого обсягу. Через випадкові збої у виробничому процесі можливий випуск партій з неприпустимо високим відсотком бракованої продукції. Визначають такі стани економічного середовища: Ө1 — придатна партія виробів; Ө2 — бракована партія виробів.
Нехай браковані вироби у придатній партії становлять 4%, у непридатній — 15 %. Проведені на підприємстві розрахунки показують, що ймовірність виробництва бракованої партії дорівнює 0,20, отже, придатна для відправлення споживачам партія має ймовірність 0,80. Таким чином, P(Θ = Ө1) = 0,80 і P(Θ = Ө2) = 0,20.
Підприємство відправляє партії товарів двом споживачам А та Б. Контрактом обумовлено, що відсоток бракованих деталей, які відправляються споживачам А та Б, не повинен перевищувати 5 та 8% відповідно. За один відсоток перевищення встановлених меж передбачається штраф розміром 100 УГО. З іншого боку, виробництво партії товарів більш високої якості збільшує витрати підприємства на 80 УГО за кожен відсоток.
Задача має два варіанти рішення (дві альтернативи): s1 — відправити партію товарів споживачеві А, s2 — відправити партію товарів споживачеві Б.
Припустимо також, що підприємець (менеджер) вирішує перевірити два вироби з усієї партії. В результаті перевірки може бути встановлено, що: 1)обидва вироби придатні; 2)один з виробів придатний; 3) обидва вироби браковані. Нехай ξ1, ξ2, ξ3 позначають ці три можливі події відповідно.
Підприємець повинен прийняти рішення: кому із споживачів— А чи Б — відправляти певну партію виробів.
Розв’язання. Функціонал оцінювання у цій ситуації доцільно подати у вигляді матриці витрат в УГО, тобто F = F-.
Рішення s1 припускає, що споживач А прийме партію виробів (5 % браку без штрафу). Якщо партія має 4% браку (Ө1), виробник зазнає збитків (5–4) 80 = 80 (УГО). Але якщо партія товарів матиме 15% браку (Ө2), то штраф становитиме (15 – 5)100 = = 1000 (УГО). Аналогічно щодо рішення s2: відправляючи споживачеві Б партію, яка містить 4% браку (Ө1), виробник зазнає збитків (8 – 4) 80 = 320 (УГО). Якщо партія містить 15% браку (Ө2), штраф становитиме (15 – 8) 100 = 700 (УГО). Отже, маємо:
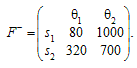
Зазначимо, що коли підприємець прагне обрати рішення, яке включає збитки від штрафу (принцип гарантованого результату за критерієм Вальда), тобто безризикове рішення, то він має відправити партію виробів споживачеві Б. (Перевірте.)
Коли підприємець приймає рішення, користуючись (це суттєво) наявною інформацією щодо P(Ө1) та P(Ө2), то, використовуючи критерій Байєса, одержимо, що sk0 = s1, тобто партію виробів доцільно відправити споживачеві А. (Перевірте.)
Відмітимо, що рішення підприємця повинно залежати від результатів ξ1, ξ2, ξ3.
Вироби можуть братися як з придатної (Ө1), так і з бракованої (Ө2) партії.

Оскільки рішення приймається після проведення контрольної перевірки, то важливим інструментом для його прийняття вже будуть імовірності, що враховують результати перевірки. Такими є апостеріорні ймовірності, що обчислюються згідно з формулою Байєса [48], а тому їх називають також байєсівськими ймовірностями:

