Методи управління (2003)

3.3.1. Матричні методи

Сутність їх - у поданні складної системи взаємовідносин між подіями, наслідками цих подій, витратами на їх реалізацію, необхідними силами та інформаційними ресурсами у формі системи взаємодії пар, трійок і т. д., які називаються матрицями. Найпростішим матрицею є двовимірна матриця типу "мета - засіб", "проблема - забезпечення". Прикладом використання двовимірних матриць може служити метод морфологічного аналізу.

Починається морфологічний аналіз з складання морфологічного класифікатора, що складається з рядків "підстава розподілу". Рядки, у свою чергу, теж діляться з яких-небудь ознаками. Основні труднощі методу - правильне складання класифікатора, досягнення смислової однозначності кожної його клітини. При цьому число визначень має бути оптимальним, щоб уникнути надмірної розробки розмірів класифікатора.

Для побудови матриць необхідно вміти точно формулювати проблему, вміти скласти перелік усіх відомих способів і засобів вирішення цієї та їй подібної проблеми, скласти перелік найважливіших характеристик параметрів ит.д.

Для морфологічного методу складним є визначення в кожен параметр Р різного числа незалежних і нерозкладних властивостей, що піддаються опису Р1, Р2, ..., Рk.

Вибираючи один з елементів кожного ряду за перспективний і поєднуючи ці елементи, отримуємо один з варіантів режиму поставленого завдання.

Тривимірні матриці представляють собою складні форми пошуку рішень в трьох вимірах, наприклад, "мета - ресурси - час".

Матричний метод може бути використаний для прийняття будь-яких рішень у будь-якій області. Він дозволяє: знайти нові невідомі рішення за межами відомих кордонів; перебрати всі можливі рішення і вибрати прийнятні; знайти наслідки, що випливають з певної причини (у загальному вигляді), або переглянути всі можливі рішення для конкретного завдання. Матриці дають матеріал і полегшують перебір значного числа варіантів рішення.

Матриця може дати рішення принципово можливі, але з різних причин нездійсненні в даний час. Вона дає несподівані комбінації рішень, які знайти іншими способами не можна.

Матриця дає безліч варіантів вирішення проблеми, але не дає сама по собі способу оцінки цих варіантів. Матричні методи дають гарні результати при дослідженні обмежених областей пошуку, але не застосовуються при вивченні погано визначених і нечітко сформульованих проблем.

Експерименти показують, що скласти матрицю (морфологічну карту) може лише той, хто володіє достатніми знаннями, уявою.

Приклади використання морфологічного методу

Приклад 1. Боротьба з мишами на дачі

У таблицю 19 зводяться всі заходи, спрямовані на боротьбу з мишами, та об'єкти, на які або через які йде вплив. Уважний перебір різних варіантів дозволяє знайти дієвий, що застосовується до реальних умов і обстановки.

Таблиця 19

Морфологічна комбінована таблиця "Боротьба з мишами"

Объекты воздей­ствия	Мероприятия
	Разорение			Преобразования
	Физи­ческие способы	Хими­ческие способы	Биологи­ческие способы	Физи­ческие способы	Хими­ческие способы	Биологи­ческие способы
Мыши-полевки	Отлов	Отрав­ление	Завести кошек. Применить болезне­творные организмы	Отлов и стери­лизация. Имитация звуковых сигналов боли и тревоги		Разведе­ние и раз­мещение на участке живот­ных — вра­гов мышей
Норы и гнезда	Механи­чески разру­шить. Затопить водой	Окурить		Заделать выходы
Пища	Удаление	Отрав­ление	Впредь не выра­щивать	Защитить растения пленкой		Выращи­вание других культур­ных расте­ний
Территория сада	Отказ от сада	Хими­ческая коренная обработ­ка почвы	Прекра­щение обра­ботки сада	Изготовле­ние ограж­дений		Перекоп­ка всего сада

Приклад 2. Дозвіл технічного протиріччя гару роботі над винаходом

Для розв'язання технічних суперечностей автор [1] запропонував морфологічну таблицю (табл. 20).

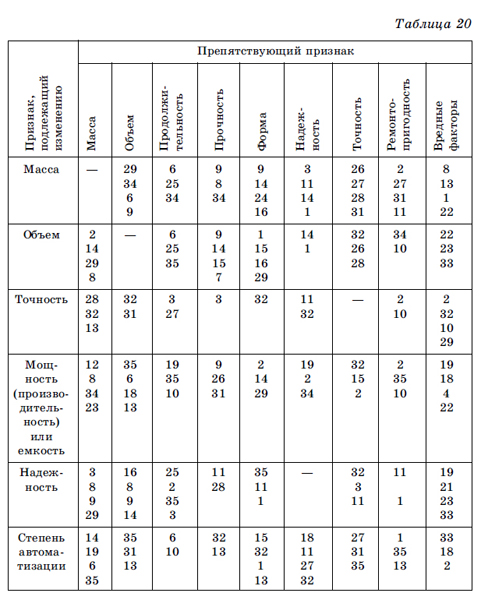
У таблиці першого варійована область відноситься до того ознакою, який необхідно змінювати, а друга - представляє ознака, що перешкоджає сприятливому вирішення проблеми. Зіставлення по 32 подібним ознаками дає 32 • 32 = 1024 можливих комбінацій.

У утворилися клітини таблиці - кожна клітина представляє певну різновид технічного протиріччя - поміщені одне або декілька вимог вирішення цієї суперечності, вже перевірених на практиці або які обіцяють успіх. На підставі матеріалів з наукової літератури складено 35 принципових рішень з поясненнями на прикладах і представлені в морфологічної комбінованої таблиці. Таблиця 13 - фрагмент з неї.

Цифри, поміщені у відповідних клітинах, позначають номер застосовуваного принципу (вимоги) рішення (номери останніх розташовуються за ступенем важливості).

Кілька прикладів із застосування таблиці.

1. Винахідника, який вирішив радикально підвищити точність

механічних годинників, займає ознака - точність.

При питанні яка буде ознака служить перешкодою при виготовленні окремих деталей треба відповідь: маса! Тому що, наприклад, механічно коливний маятник-баланс із-за своєї маси навряд чи дозволяє розраховувати на більш постійні коливання.

Ці відповіді призводять до клітки, відповідної комбінації "точність - маса". У цій клітці вказані вимоги до рішення 28, 32 і 13. Вимога 28 говорить: "Заміна механічної енергії", а роз'яснення до нього: "Замість механічної системи слід застосувати електричну, магнітну, оптичну або гідропневматичне". Воно наводить на думку про необхідність застосувати для вимірювання часу коливальну систему іншого виду, можливо коливання кристала кварцу або коливання атома.

2. При монтажі електропроводки в якомусь будинку важливо

забезпечити безпеку при перевантаженнях і можливість просто -

го ремонту.

Який ознака слід змінювати? Надійність.

Який ознака служить перешкодою при традиційному способі рішення (наприклад, за рахунок збільшення поперечного перерізу кабелю)? Зручність ремонту.

Відповідна клітина таблиці містить вимоги 11 і 1.

Вимога 11 означає: "Запобігання (профілактика)", а додаткове роз'яснення: "Передбачити можливість аварії заздалегідь і забезпечити заходи зі зменшення шкоди".

Тепер до відомого рішення - застосувати плавкі запобіжники або автомати - короткий шлях.

Подібних прикладів має бути достатньо, щоб морфологічна таблиця стала "каталізатором ідей". Особливо важливою є правильна постановка питання. Якщо формулювання питання не приводить до мети, її треба змінити. Таким чином, якщо мова йде про знаходження цілої "системи варіантів рішень", то морфологічний метод можна застосовувати незалежно від конкретного завдання, для вирішення якої він був призначений.

Прийняття рішень з використанням матриць і таблиць

Суть ухвалення рішення - вибір найкращої з декількох альтернативних по конкретних, заздалегідь встановленим критеріям.

Використовувані в практичній діяльності матриці і таблиці вносять організуючий початок в прийоми і способи інтелектуальної діяльності осіб, які приймають рішення. Вони є методами статистичної теорії рішень. Викладаючи цей матеріал, ми ставимо собі за мету не стільки навчити користуватися цими методами, скільки допомогти зрозуміти суть цих інструментів.

Платіжна матриця

Платіж - це отримання грошової суми за вироблений товар або надану послугу в реальних умовах обстановки. Зобразивши, з одного боку, гроші, з іншого-конкретні обставини, коли вони виплачуються, отримаємо платіжну матрицю. Матриця додає наочність залежності платежу від певних подій. Якщо цієї події не трапляється, то платіж стає іншим.

Матрицю корисно використовувати у разі, коли:

Особа, що приймає рішення, має можливість мати об'єктивну оцінку подій і має можливість розрахунку їх ймовірності.

Результати прийнятого рішення залежать від обраної альтернативи та подій, що відбуваються.

При ухваленні рішення максимально враховується ймовірність події. Імовірність можна розрахувати з використанням методів теорії ймовірності, чи суб'єктивно оцінити, виходячи з простих тенденцій (метод екстраполяції) або на основі власного досвіду в подібних ситуаціях.

Якщо ймовірність не враховується, то прийняте рішення буде зісковзувати у бік оптимістичних наслідків. Наприклад, виходячи з того, що зараз в Україні, вклавши капітал в торговельно-закупівельну діяльність, можна отримати прибуток у сотні відсотків, а у виробничу - лише 8-10%, потрібно займатися першим. Однак, з огляду на ймовірність залежності сьогоднішніх реалій від корупції, рекету до можливості інвестування економіки та отримання пільгових кредитів, варто ще подумати.

Наочний приклад використання платіжної матриці запропонований у популярному підручнику [48].

Приклад. Торговий агент вирішує, йому летіти літаком до споживача або їхати поїздом. Якщо погода буде гарною, то можна летіти і витратити на дорог 2 часа замість 7 годин поїздом. Якщо поїде поїздом, то втратить день на роботі, який міг би збільшити збут на 1500 доларів. За оцінкою, іногородній споживач повинен дати замовлення на 3000 доларів, якщо агент особисто відвідає клієнта. Якщо літак не злетить через туман, це знизить замовлення до 500 доларів. Правда, в цьому випадку і вдома можна забезпечити замовлення на 1500 доларів (табл. 21).

Таблиця 21

Вероятность погоды	Туман (0,1)	Ясно (0,9)
Самолет Поезд	2000 долларов 3000 долларов	4500 долларов 3000 долларов

Наведені вище дані платіжної матриці відображають оцінку наслідків варіантів дій торгового агента.

Торговий агент, бачачи, що ймовірність ясної погоди в 10 разів вище, ніж туману і (9 шансів з 10) що він продасть товарів на 4500 доларів, приймає рішення летіти літаком.

Таблиця оцінок

Надає можливість наочно відобразити оціночні характеристики різних альтернатив.

Розглянемо суть методу на прикладі покупки автомобіля. Бажаючи купити автомобіль, ми як критерій керуємося: потужністю мотора, ціною та зовнішнім виглядом.

Потужність мотора висловимо в кінських силах, ціну в доларах. Для оцінки зовнішнього вигляду приймемо систему балів: 5 - відмінно, 4 - добре, 3 - задовільно, 2 - посередньо, 1 - незадовільно. Щоб привести ці різні критерії до єдиної системи оцінок, поставимо собі діапазонами абстрактних одиниць. Приймемо як оптимальної найбільшу або найменшу суму безрозмірних одиниць.

Наприклад, візьмемо найменше значення суми трьох критеріїв - зростання величини будь-якого критерію означатиме погіршення.

Занесемо різні відповідності розмірних і безрозмірних характеристик в табл. 22.

Таблиця 22

Мощность	Безраз-	Цена,	Безраз-	Безраз-	Внешний
мотора,	мерная	долларов	мерная	мерная	вид,балл
лошад.	шкала		шкала	шкала
силы
10	1	500	1	1	1
40	2	1000	2	1	2
70	3	3000	3	1-2	3
100	4	3800	4	2	4
130	5	4000	5	2-3	5
160	6	4200	6	3	6
190	7	4400	7	3-4	7
210	8	4600	8	4	8
250	9	4800	9	4-5	9
300	10	5000	10	5	10

Замість заданих характеристик можна підставити безрозмірні одиниці (табл. 23).

Насправді на вибір впливає якийсь один критерій. Наприклад, ціна або суб'єктивна думка дружини чи тещі, яка фінансує покупку.

Це вимагає внесення в табл. 23, де передбачалася однакова значущість критеріїв, вагових коефіцієнтів. У табл. 24 коефіцієнти представлені у другому стовпчику.

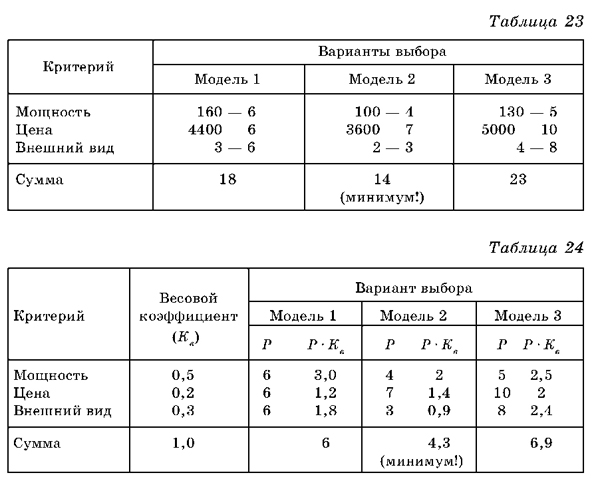
Ціна, як найбільш важливий критерій, отримує найменше значення коефіцієнта (0,2); зовнішній вигляд - дещо більше (0,3), а потужність - (0,5).

Вносимо безрозмірні характеристики для кожної моделі машини з таблиці 16 і множимо їх на вагові коефіцієнти, що відповідають трьом критеріям. Підрахуємо суми цих творів для кожної моделі і знайдемо мінімум. При такому підході до вибору варіанту покупка другої моделі - найкраще рішення.

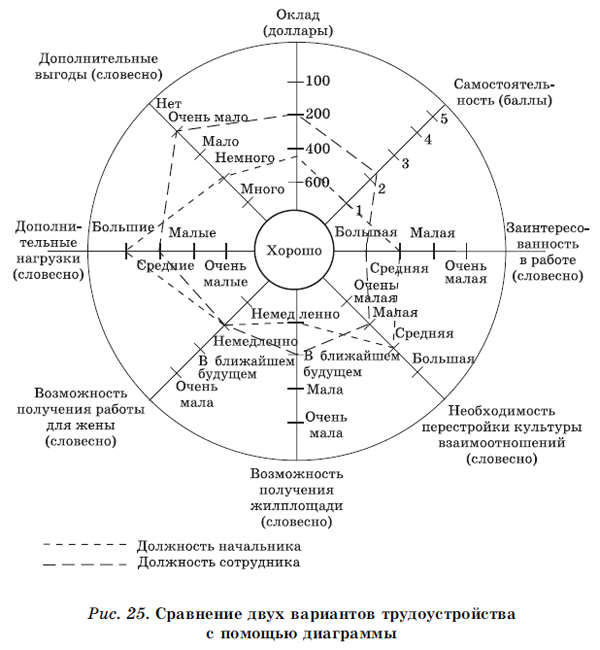
3.3.2. Прийняття рішення з використанням діаграми, побудованої в полярних координатах

Це спосіб відображення результату прийняття рішення з декількома критеріями і двома варіантами. Уявімо подібне рішення на прикладі (рис. 25).