Внутрішній економічний механізм підприємства (2001)

Питання адаптації операційної системи підприємства до зміни обсягу зайнятості досі вивчалося нами лише в технічному аспекті. Розглядались технічно можливі варіанти досягнення заданих обсягів роботи, кожен з яких характеризувався певною кількістю одиниць обладнання, часом та інтенсивністю його використання. Наступним етапом у дослідженні вказаної проблеми має стати розгляд питання, пов’язаного з економічною ефективністю процесу адаптації. Процес адаптації вважається економічно ефективним, або оптимальним, якщо з усіх технічно можливих варіантів він виявляється найдешевшим для підприємства, тобто загальні витрати, що пов’язані з випуском заданої кількості кінцевої продукції, є мінімальними. Задача оптимальної адаптації агрегатів за критерієм мінімуму витрат на даний момент не має вичерпного розв’язку. Нижче розглядається механізм оптимальної адаптації для деяких постановок цієї задачі.

Припустимо, що при виготовленні продукції використовується М функціонально різних типів агрегатів. Для виконання роботи в розпорядженні підприємства є тільки одна машина кожного типу.

Формула загальних витрат виробництва, у даному разі матиме такий вигляд:

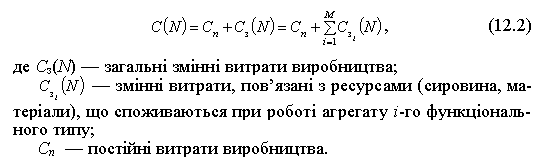
У свою чергу, постійні витрати виробництва можна зобразити як суму загальних витрат, необхідних для підтримування виробничої готовності підприємства, позначених символом, та загальних витрат, пов’язаних з використанням засобів праці (агрегатів). Останні можна подати у вигляді суми витрат на використання та експлуатацію для окремих груп агрегатів залежно від їх функціонального типу (у нашому випадку в кожну групу входить по одній машині). Таким чином, вираз (12.2) трансформується у вираз:

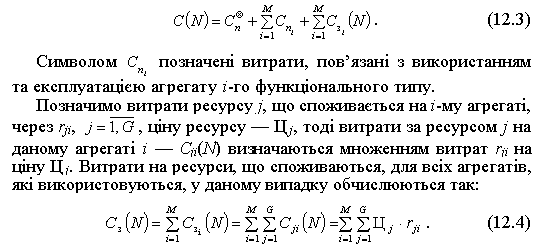
Наведену формулу можна записати трохи інакше, якщо витрати j-го ресурсу на і-му агрегаті rjі виразити через норму витрат j-го ресурсу на одиницю кінцевої продукції на і-му агрегаті aji та обсяг виконаної на цьому агрегаті роботи N.

Цілком очевидно, що rjі = ajiN. Норма витрат аjі, взагалі кажучи, не є величиною постійною. Вона залежить від технічних параметрів роботи агрегату, серед яких особливе місце займає інтенсивність його використання .

Припускаючи всі технічні параметри роботи агрегату за винятком інтенсивності  незмінними, норму витрат аjі можна вважати величиною, залежною лише від інтенсивності:

Загальні витрати виробництва С(N) будуть мінімальними для даного обсягу випуску, якщо будуть мінімальними витрати на ресурси, що споживаються, за всіма типами агрегатів Сз(N).

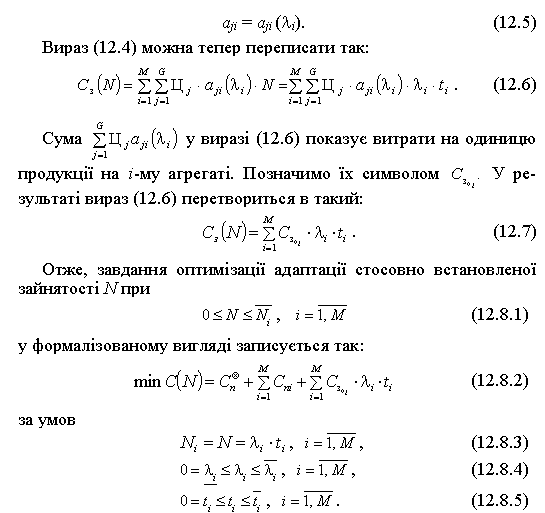
Через те, що в даній постановці задачі є тільки одна машина кожного функціонального типу, то в межах типу агрегату, який застосовується, немає кількісної адаптації. Це означає, що мінімізація загальних витрат виробництва заданого обсягу випуску N здійсненна шляхом оптимального вибору величини часу роботи tі та інтенсивності використання і, за яких витрати на ресурси, що споживаються, по кожному агрегату і є найменшими.

Розглянемо зміну величини витрат при адаптації певного агрегату за часом та інтенсивністю.

Графік указаної функції наведено на рис. 12.2. На ньому видно, що функція Cti є нелінійною, зростаючою, має дві ділянки опуклості: спочатку вона опукла уверх, а потім униз.

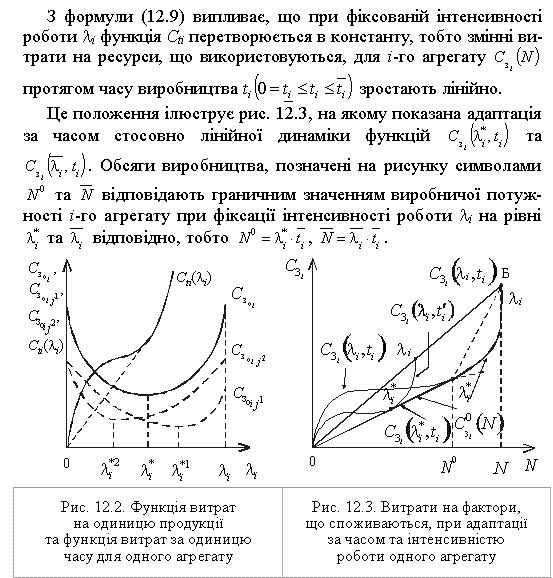
Тепер від розгляду витрат при комбінованій адаптації для одного агрегату перейдемо до питання мінімізації витрат на експлуатацію обладнання при комбінованій адаптації для кількох функціонально однакових агрегатів.

Передусім зауважимо, що для вказаної проблеми можливі різні формулювання задач. Нехай у розпорядженні підприємства для виготовлення кінцевої продукції є кілька агрегатів (машин) одного функціонального виду, але таких, що потребують різних витрат: n = 1, …, L. Агрегати одного і того самого виду розрізняються між собою функціями витрат на одиницю продукції

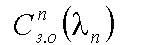
У зв’язку з цим постає завдання комбінованої адаптації, суть якого полягає у визначенні відповідних адаптаційних параметрів операційної системи підприємства (комбінація агрегатів із наявних на підприємстві, інтенсивність та час їх роботи) для виготовлення необхідної кількості кінцевої продукції N з найменшими витратами.

У формалізованому вигляді задача може бути представлена так:

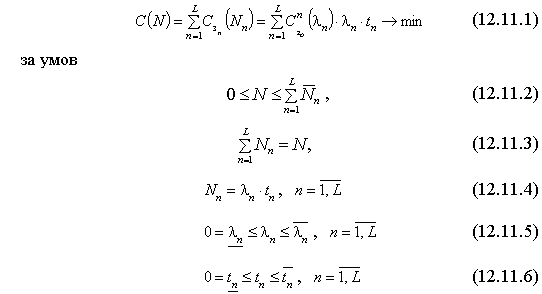
З урахуванням сказаного функції витрат агрегатів Cзn(Nn) можуть бути специфіковані так:

Розглянемо далі числовий приклад оптимізації комбінованої адаптації до зміни обсягу кінцевої продукції [12, c. 467]. Вихідні дані прикладу подано в табл. 12.1.

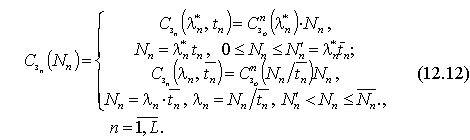
З табл. 12.1 видно, що в прикладі припускається наявність двох (n = 1, 2) функціонально однакових, але різних за витратами агрегатів. Максимальний час роботи агрегатів — 8 год. Максимальна інтенсивність їх роботи різна і становить 22 та 23 одиниці продукції за годину для першого і другого агрегатів відповідно. Задача розв’язується у два етапи. На першому етапі попередньої оптимізації формулюються функції витрат для кожного агрегату з урахуванням їх адаптації за часом та інтенсивністю роботи. На другому етапі здійснюється основна адаптація, тобто визначається мінімальне за витратами використання обладнання.

Згідно з (12.12) вони відповідають змінним витратам і одночасно є граничними витратами виробництва на агрегатах на проміжку адаптації за часом. Функції витрат машин для часової адаптації одержуємо шляхом їх множення на обсяг випуску Nn.

Другий етап основної оптимізації може здійснюватися двома шляхами. Перший шлях базується на функціях граничних витрат, а другий використовує метод динамічного програмування. Далі, в продовження запропонованого прикладу, детально викладається процес оптимальної адаптації за допомогою функцій граничних витрат. Для методу ж динамічного програмування буде вказана лише його загальна схема без розгляду практичного прикладу.

Нагадаємо, що сформульована раніше задача адаптації агрегатів з різними витратами за їх кількістю, часом та інтенсивністю роботи не припускає постійних витрат, пов’язаних з роботою засобів праці.

Отже, розподіл виробництва продукції з мінімальними витратами здійснюється так. Спочатку потрібно завантажити агрегат з найменшими граничними витратами. Обсяг випуску, що закріплюється за ним, можна збільшувати доти, доки дозволяє його потужність, а граничні витрати не перевищують найменших граничних витрат якого-небудь іншого агрегату при адаптації за часом. Коли остання умова не виконується, завантажується відповідний агрегат з найменшими граничними витратами. Таким чином виробництво продукції розподіляється між машинами в порядку менших витрат у межах їх потужності.

З табл. 12.3 видно, що агрегат 1 має менші граничні витрати при адаптації за часом. Отже, він включається в роботу першим з оптимальною інтенсивністю λ = 18.

Сутність методу динамічного програмування для комбінованої адаптації до заданого обсягу випуску N полягає в тому, щоб послідовно розподілити його виробництво між наявними агрегатами на частини Nn. Критерієм оптимізації в цьому випадку є загальні витрати виробництва. Кожний етап оптимізації здійснюється включенням у розрахунок наступного агрегату. За допомогою цього методу задача (12.11.1) – (12.11.6) з L змінними Nn поділяється на L взаємозалежних часткових задач, кожна з яких має одну змінну. На основі рішення цих часткових задач рекурсивно визначаються оптимальні Nn для заданого N. Нехай L агрегатів уключаються в розрахунок у порядку 1…, n, …, L, тоді схема визначення оптимальних обсягів випуску Nn за допомогою динамічного програмування запишеться так:

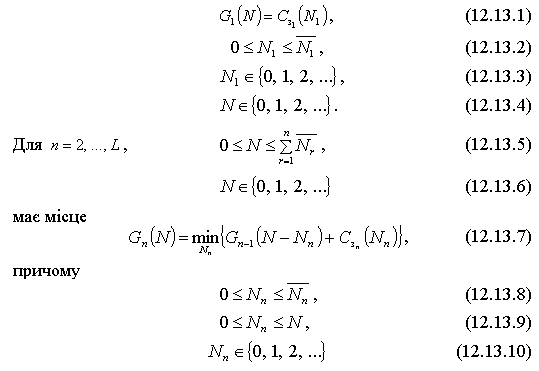
На першому етапі розв’язується функція витрат Cз1(N1) агрегату, який уводиться в роботу першим; при цьому враховується межа потужності (обмеження (12.13.2)) та береться дискретне цілочисельне змінення кількості продукції N1 (обмеження (12.13.3)). Ця функція позначена як G1(N). На другому етапі в розрахунок уводиться другий агрегат. Заданий цілочисельний обсяг випуску N розподіляється між двома машинами з урахуванням досягнення найменших витрат,

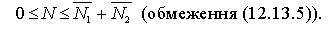
Знову береться до уваги межа потужності, дискретне цілочисельне змінення рівня зайнятості (обмеження 12.13.8, 12.13.10).

На n-му етапі в розрахунок уводиться n-ий агрегат (n = 1, …, L). Обсяг випуску кінцевої продукції N на цьому етапі розподіляється за критерієм мінімуму витрат (формула 12.13.7) між агрегатом n, який щойно залучається і на який припадає Nn одиниць продукції та раніше задіяними на n-1 етапах розрахунку n-1 агрегатами з випуском N – Nn. Процес розподілу закінчується після виконання L етапів розрахунку.