Мікроекономічна теорія виробництва і витрат (2003)
3.2. Показники заміщуваності та доповнюваності факторів виробництва
Нехай у виробництві задіяно два види змінних ресурсів Х та Y і виробнича функція описується ізоквантами, наведеними на рис. 3.7, а.
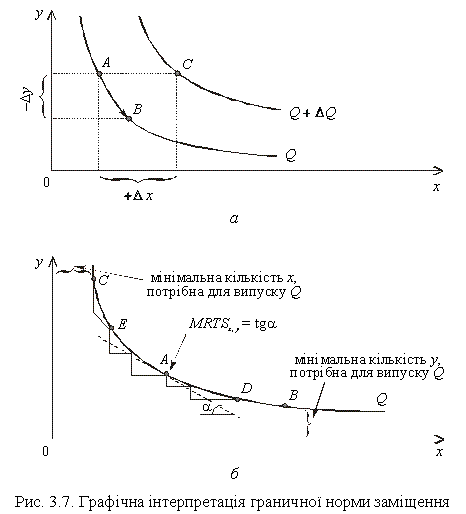
За переходу від комбінації ресурсів, позначених точкою А, до комбінації в точці В, міру замінності ресурсу y ресурсом х характеризує та кількість ресурсу y (–y), що компенсується збільшенням кількості ресурсу х (+х) за руху вниз уздовж ізокванти. Розмір –(∆y/∆x) є нахилом ізокванти і називається нормою технологічної заміни фактора y фактором х. Знак мінус показує, що скорочення витрат фактора y, за умови незмінності випуску, вимагає збільшення витрат фактора х. Якщо виробнича функція диференційована і зміни факторів (Δх і Δy) можуть набирати як завгодно малих значень, то норма технологічної заміни наближається до значення нахилу дотичної до будь-якої точки ізокванти lim (∆y/∆x, коли ∆x→0, що й дозволило назвати її граничною нормою технологічного заміщення (Marginal rate of technical substitution, MRTS). Це унаочнює рис. 3.7, б, з якого видно, що нахили дотичних до точок С, Е, А, D, В істотно різняться. У точці А нахил дотичної, тобто гранична норма заміни фактора у фактором х (MRTSx, y), дорівнює tgα.
Математично MRTSx, y можна знайти, беручи першу похідну по х від рівняння, що визначає ізокванту:
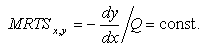
Наприклад, якщо ізокванта визначається виразом 100 = х у, то гранична норма заміни фактора у фактором х може бути знайдена в такий спосіб:
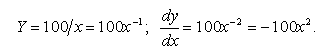
Підставляючи різні значення х, знаходимо MRTSx, y у різних точках ізокванти. В мікроекономічній теорії виробництва, як правило, оперують не неперервною, а дискретною MRTS, розглядаючи збільшення х на одиницю. З огляду на те, що традиційно використовується двофакторна виробнича функція, в якій максимальний обсяг виробництва забезпечується використанням визначеної кількості праці і капіталу, розраховують норму заміни капіталу працею або праці капіталом.
Гранична норма технологічної заміни капіталу працею визначається величиною капіталу, що її може замінити одиниця праці, не викликаючи при цьому зміни обсягу виробництва. Аналогічно можна сформулювати визначення для граничної норми заміни праці капіталом.
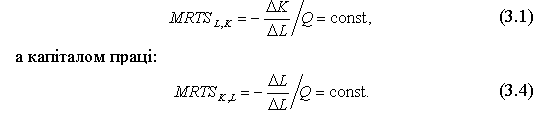
Для ізокванти, побудованої за даними виробничої сітки (табл. 3.1) і наведеної на рис. 3.8, гранична норма технологічного заміщення працею капіталу за переходу з комбінації, позначеною точкою А, у комбінацію В дорівнюватиме
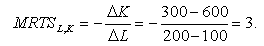
Це означає, що у разі зменшення витрат капіталу з 600 до 300 машино-год 1 од. праці може замінити 3 од. капіталу.
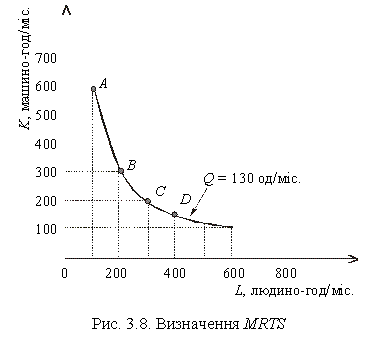
Гранична норма технологічного заміщення зменшується в міру руху вниз уздовж ізокванти — один ресурс замінюється іншим у прогресивних кількостях. У табл. 3.2 наведено результати розрахунку граничної норми технологічного заміщення працею капіталу для ізокванти, що характеризує обсяг випуску Q = 130 приладів на місяць (див. рис. 3.8).

Кожна точка ізокванти — комбінація факторів, що характеризує технологію. За переходу від капіталомістких до трудомістких технологій кожна година праці може заміщати все меншу й меншу кількість годин роботи машин. Розглянемо це на прикладі співвідношення витрат праці і капіталу за виготовлення обшивок фюзеляжу літака. Нехай прес, обслуговуваний одним пресувальником, перетворює лист алюмінієвого сплаву на обшивку фюзеляжу за кілька секунд. Цю ж обшивку можна виготовити штампуванням гумою, використовуючи менш продуктивне і дешевше устаткування, що обслуговується двома робітниками. Нарешті, лист алюмінію можна перетворити на обшивку подвійної кривизни вибиттям його бляхарями вручну по болванці. Зрозуміло, що це візьме багато часу за низької якості продукції. Отже, чим більше праці і менше капіталу використовується у виробничому процесі, тим сутужніше заміщати капітал працею без зниження випуску і якості виробів. Це справедливо не тільки щодо заміщення капіталу працею, а й щодо заміщення праці капіталом, а також стосовно до інших ресурсів. Тобто, спадання граничної норми технологічного заміщення одного ресурсу іншим — феномен, властивий більшості виробничих процесів. Іноді цю емпіричну закономірність називають законом спадання граничної норми заміщення. З практичного погляду він може бути інтерпретований так: за зростаючої диспропорціональності обсягів застосування факторів унаслідок зміни їхньої віддачі заміщуваність стає все менш вигідною. Заміщеність між двома факторами має сенс, допоки гранична норма їхнього заміщення буде більше нуля. Тому межу заміщеності на ізокванті позначають точками, для яких MRTSx, y = 0. Вони відповідають точкам В та С на рис. 3.7, б.
Правило заміщення факторів. Гранична норма технологічної заміни пов’язана з граничними продуктами обох факторів. Звернемося знову до рис. 3.7, а. Припустимо, що, знаходячись на ізокванті Q у точці А, ми збільшили витрати фактора х на розмір х. У такому разі ми перейдемо в точку С, що лежить на ізокванті Q + Q. Приріст випуску дорівнюватиме величині добутку х на граничний продукт фактора х (МРх):
Q=xMPx
Але, за визначенням MRTS, ми повинні залишитися на тій самій ізокванті Q. Щоб повернутися на вихідну ізокванту, збільшення обсягу застосування фактора х має бути компенсовано зниженням обсягу застосування фактора у. Втрати випуску дорівнюють добутку величину вивільненого фактора –у на граничний продукт фактора у (МРу):
-Q= -y*MPy
Оскільки, за визначенням, необхідно залишитися на тій самій ізокванті, то приріст випуску має дорівнювати його зниженню:
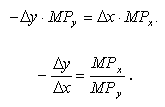

Ми розглянули ситуацію з двома змінними факторами виробництва. Отримані результати неважко перенести на n-мірний випадок. Припустимо, що в багатофакторній виробничій функції нас цікавить заміщення ресурсу і-го виду ресурсом j-го виду. Необхідно зафіксувати обсяги застосування всіх інших видів ресурсів і як змінні розглядати і-й та j-й ресурси. Ізоквантна варіація в даному випадку характеризуватиметься рухом уздовж ізокванти, розміщеної на площині з координатами xi, xj (на осі ординат ресурс, припустимо, і, на осі абсцис — j). Усі міркування аналогічні наведеним, і гранична норма заміни ресурсу і ресурсом j — це кількість і-го ресурсу, яка може бути вивільнена “в обмін” на збільшення застосування j-го ресурсу на одиницю так, щоб загальний обсяг продукції залишився незмінним:
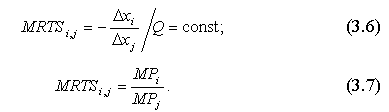
Граничну норму технологічної заміни іноді називають коефіцієнтом заміщення, або коефіцієнтом субституції факторів виробництва.
Ступінь доповнюваності факторів виробництва та її співвідношення з MRTS. Багато факторів виробництва не тільки заміщують, а й доповнюють один одний. Кривизна ізоквант відбиває труднощі, що виникають у разі заміни одного фактора іншим і водночас характеризує ступінь доповнюваності факторів. Співвідношення між доповнюваністю і заміщеністю факторів різні в різних галузях промисловості і навіть в одній галузі, але для різних видів виробництв. Наприклад, на складальних роботах відносно просто можна замінити складальних роботів ручною працею із застосуванням механізованого інструменту або ж реалізувати будь-яку комбінацію праці і капіталу, тобто фактори мають властивості і доповнюваності, і заміщеності. А от заміна капіталу працею в хімічній промисловості, в різних апаратурних процесах практично неможлива. Тут діють чіткі співвідношення доповнюваності: один апарат обслуговується, наприклад, трьома робітниками.
Ступінь доповнюваності факторів звичайно вимірюють коефіцієнтом доповнюваності — KD. Так, KDLK показує, в яких розмірах праця може доповнювати капітал для ізоквант певного виду. Математично ступінь доповнюваності факторів виражається через другу похідну фактора y по фактору х, тобто вона відповідає величині вигину ізокванти в кожній її точці:
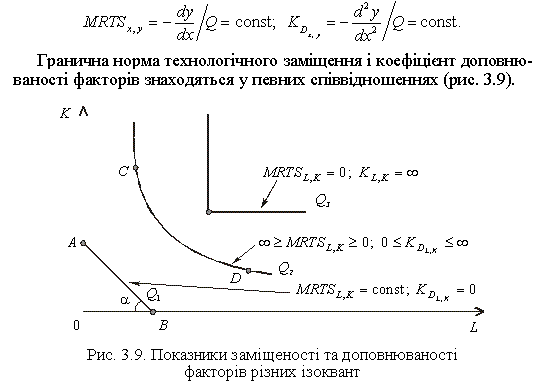
Лінійна ізокванта передбачає ідеальну, повну, досконалу заміщеність факторів. Наприклад, для того, щоб отримати обсяг випуску Q1 (див. рис. 3.9), може бути використаний або капітал (точка А), або праця (точка В), або будь-яка комбінація їх на лінії АВ за постійної норми заміщення, яка дорівнює tga=OA/OB Якщо на осях відтиняються рівні відрізки, то tga=1 якщо ОА < ОВ — tga<1 якщо ОА > ОВ — tga>1 але в будь-якому разі MRTS = const. Оскільки за абсолютної заміщеності факторів, що описується лінійною ізоквантою, гранична норма заміщення факторів дорівнює постійному розміру, то коефіцієнт доповнюваності дорівнює 0.
Неперервна (субституційна) ізокванта (наприклад, Q2 на рис. 3.9) припускає заміщення ресурсів у визначених інтервалах, за межами яких заміщення одного фактора іншим або технічно неможливе, або економічно не ефективне (точки С та D). Конфігурація такої ізокванти припускає необмежену подільність застосовуваних ресурсів і спадну граничну норму технічного заміщення капіталу працею. Оскільки гранична норма заміщення працею капіталу варіює від нуля (точка D) до нескінченності (точка С), то і коефіцієнт доповнюваності капіталу працею може змінитися від ∞ до 0.
Ізокванта леонтьєвського типу (на рис. 3.9 — Q3), що характеризує жорстку взаємодоповнюваність факторів, має MRTSL, K = 0 і відповідно, KDLK = безкінечність
Зрозуміло, що поняття “доповнюваність” і “заміщеність” не виключають одне одного. Фактори можуть доповнювати один одного і бути водночас взаємозамінними. При цьому зі збільшенням ступеня доповнюваності рівень заміщеності знижується, і навпаки.