Кількісні методи в управлінні інвестиціями (2000)
1.2. Прості і складні проценти
Простий процент обчислюється за такою формулою (1.1):
I = Pіt, (1.1)
де I — величина прибутку власника інвестицій;
i — процентна ставка;
t — період часу інвестування;
P — первісна сума інвестиції (вкладу).
Сутність методу нарахування за простими процентами зводиться до того, що проценти нараховуються впродовж усього терміну інвестицій (кредиту) на ту саму величину капіталу, що інвестується. Наприкінці періоду t сума, одержувана інвестором, дорівнює P + I. Тоді:
S = P + I = P + Pit = P(1 + it). (1.2)
Величина (1 + it) зветься множником нарощування простих процентів.
t=n/K, (1.3)
де n — число днів функціонування угоди;
К — часова база (кількість днів у році).
В цьому разі формула (1.2) набуде такого вигляду:
S=1+i*n/K (1.4)
В ряді країн для зручності обчислень рік триває 360 днів. Це так звана «німецька практика». Проценти, що розраховані за часовою базою K = 360 днів, називаються звичайними чи комерційними.
Існує також «французька практика», коли тривалість року К = 360 днів, а тривалість місяців за днями відповідає календарному обчисленню. І, нарешті, в цілій низці країн використовується «англійська практика», що враховує тривалість року К = 365 днів, а тривалість місяців року — згідно з календарним обчисленням.
При математичному дисконтуванні розв’язується задача, зворотна визначенню нарощуваної суми. Сформулюємо її таким чином: яку суму необхідно інвестувати на t років, щоб при нарахуванні на неї процентів за ставкою і отримати суму, що дорівнює S.
Використовуючи формулу (1.2) розрахунку нарощуваної суми за простою процентною ставкою, отримаємо:
P=S*1 / (1 + it)
де знаменник 1 / (1 + it) — дисконтний множник, що показує, в скільки разів первісна сума є меншою від нарощеної.
Випишемо низку похідних формул з формули (1.5):
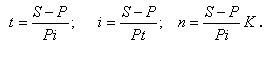
Метод нарахування по складних процентах полягає в тому, що в першому періоді нарахування здійснюється на первісну суму інвестицій (кредиту), після цього вона складається з начисленим процентом і в кожному наступному періоді проценти нараховуються на вже нарощену суму. Тож база для нарахування процентів постійно змінюється.

● Приклад 1. Нарахування складних процентів
$2000 інвестуються під 12% річних на 10 років. Визначте суму, яка акумулюється наприкінці 10-го року.
Розв’язання. Використовуючи рівняння (1.7), отримаємо:
S10 = $2000(1 + 0.12)10 = $2000 (3.1058) = $ 6211.70.
Наприкінці десяти років можна отримати $6211.70.
Якщо впродовж терміну угоди процентні ставки змінюються в часі, але в певні терміни, то нарощена сума в цьому разі визначається за формулою:
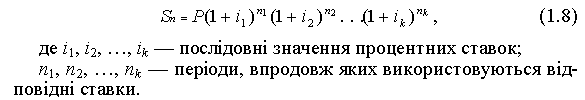
Використання у фінансових розрахунках простих і складних процентів дає неоднакові результати. Відмінності в них зумовлені термінами угод. При рівній величині простої і складної процентної ставки (iп = iс) та при терміні позички (інвестування) меншому 1 року (n < 1), нарощена сума, обчислена за простими процентними ставками, буде більшою за нарощену суму, обчислену за складними процентами, тобто 1 + iп n > (1 + iс)n. При терміні угоди більшому за рік (n > 1) нарощування за складними процентами випереджає нарощування за простими, тобто (1 + iпn) < (1 + iс)n.
● Приклад 2. Співвідношення нарощених сум, обчислених за простими та складними процентами
Нехай проста і складна процентні ставки є рівними (іп = іс = і). Довести, що при n < 1 нарощена сума, що обчислена за простими процентами, буде більшою від нарощеної суми, обчисленої за складними процентами, а при n > 1 — навпаки.
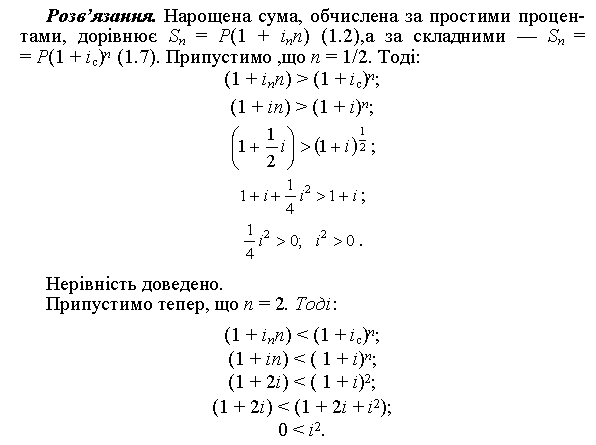
Нерівність доведено.
Використовуючи множники нарощування за простими і складними процентними ставками, визначимо час, необхідний для збільшення первісної суми в N разів.
Щоб первісна сума P збільшилася в N разів, потрібно, щоб множники нарощування дорівнювали N, тобто:
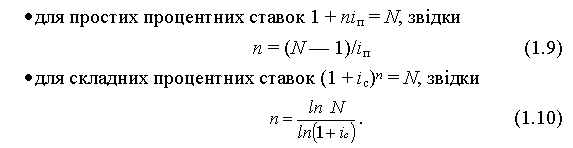
● Приклад 3. Термін збільшення первісної суми інвестицій в N разів
Розрахуйте термін збільшення первісних сум інвестицій в 3 рази, використовуючи множники нарощування за простими та складними процентами. Річна процентна ставка — 6%.
Розв’язання. Для розрахунку терміну збільшення первісної суми інвестицій у 3 рази, використовуємо формули (1.9) та (1.10).
Для простої процентної ставки — 6% маємо (1.9):
Для складної процентної ставки –6% маємо (1.10):
n=ln3/ln(1+0.06)=1.0986/0.0582=18.9 років.
Тож для збільшення первісної суми інвестицій у 3 рази при річній простій процентній ставці 6%, потрібні 33 роки і 4 місяці, а при річній складній процентній ставці 6% — 18 років та 11 місяців.
В депозитних угодах, у контрактах на отримання кредиту передбачається капіталізація процентів декілька разів на рік по півріччях, кварталах, інколи щомісячно. Однак квартальні чи місячні процентні ставки не вказуються, а вказується річна процентна ставка, яку називають номінальною. Крім того, зазначається кількість періодів нарахування процентів на рік — m. Якщо n —кількість років, то R = mn — кількість періодів нарахування процентів за весь термін угоди (контракту). Тоді для нарахування відсотків m разів на рік використовується формула (1.11):
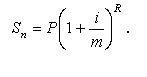
● Приклад 4. Нарахування нарощеної суми за складними процентами
Інвестор вклав $3000 в банк при 10% річних на 5 років на умові нарахування складних процентів щокварталу. Яку суму він отримає в кінці 5-річного періоду?
Розв’язання. Використовуючи формулу (1.11), отримаємо:
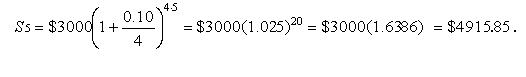
Ефективна ставка вимірює той реальний відносний прибуток, що одержує кредитор (інвестор) у цілому за рік. Ефективна ставка, іншими словами, відповідає на питання, яку річну ставку складних процентів необхідно встановити, щоб отримати такий самий фінансовий результат, як і при m-разовому нарахуванні процентів за рік за ставкою i/m.
Позначимо ефективну ставку Iе.
Рівність нарощуваних сум буде забезпечена в тому разі, якщо рівні первісні суми P, періоди нарощування n і множники нарощування, тобто:
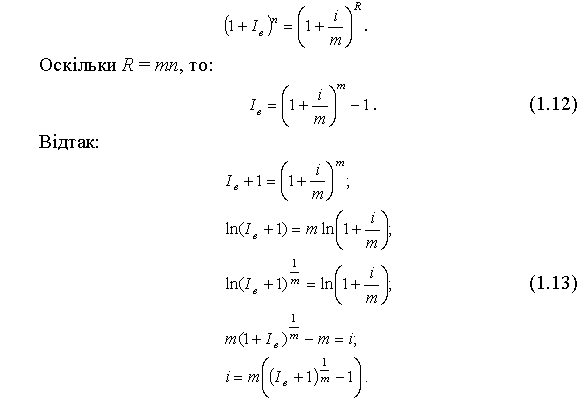
● Приклад 5. Визначення ефективної ставки складних процентів
Визначити ефективну ставку складних процентів з тим, щоб отримати таку ж нарощену суму, як при використанні номінальної ставки і = 20% при щоквартальному нарахуванні процентів (m = 4).
Розв’язання. Використовуємо формулу (1.12):
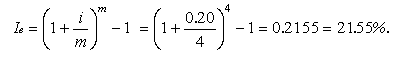
Таким чином, ефективна ставка складних процентів дорівнює 21.55%.