Кількісні методи в управлінні інвестиціями (2000)

Нарахування процентів на первісний капітал, або дисконтування нарощуваних сум, може здійснюватися так часто, що цей процес можна розглядати як безперервний. У цьому разі використовується нарахування безперервних процентів.

Суть безперервних процентів у тому, що кількість періодів нарощування чи дисконтування прагне до нескінченності, а часовий інтервал між періодами — до нуля.

Безперервне нарощування процентів здійснюється за допомогою особливого виду процентної ставки, пойменованої силою зростання. Сила зростання — це відносний приріст нарощуваної суми в нескінченно малому проміжку часу.

Формула обчислення нарощуваної суми при нарахуванні безперервних процентів має такий вигляд:

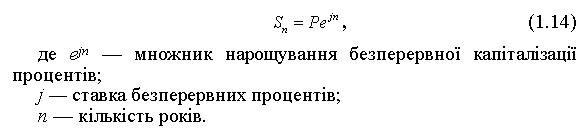
● Приклад 6. Нарахування безперервних процентів

Вкладник помістив $6000 у банк на 7 років під 8% щорічних на умові безперервного нарахування процентів. Яку суму отримає вкладник через 7 років?

Розв’язання. Використовуємо формулу (1.14):

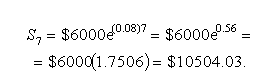
В кінці сьомого року вкладник отримає $10504.03.

Оскільки безперервні та дискретні проценти функціонально пов’язані один з одним, то можна записати рівність множників нарощування:

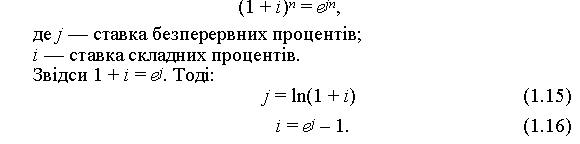
● Приклад 7. Порівняння ставок безперервних і складних процентів

Вкладник помістив гроші в банк під 8% щорічних на умові нарахування складних процентів. Якою повинна бути ставка безперервних процентів, щоб вкладник одержав ту ж суму ,як і при нарахуванні складних процентів?

Розв’язання. Використовуємо формулу (1.15):

j = ln(1 + i) = ln(1 + 0.08) = ln(1.08) = 0.0770 = 7.70%.

Безперервна ставка має дорівнювати 7.70%.