Кількісні методи в управлінні інвестиціями (2000)

При використанні процедур дисконтування грошових потоків при оцінці інвестицій необхідно знати теперішню (інші назви — сучасну, наведену, поточну) вартість грошової суми, що може бути отримана в майбутньому. Якщо ми візьмемо формулу визначення майбутньої вартості грошей (1.7), то з неї ми можемо отримати вираз для розрахунку теперішньої вартості грошей:

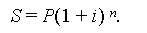
Нехай для зручності P = PV. Тоді PV — це теперішня вартість суми Sn, яку можна отримати, якщо б сума PV була вкладена на n років за складною процентною ставкою i:

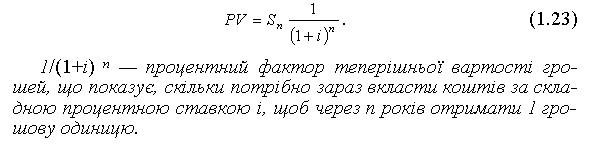
В багатьох задачах, що постають на практиці, грошові кошти повинні надходити або вкладатися в кінці кожного року за певний проміжок часу. Теперішня вартість ряду платежів (або надходжень) є сумою щорічних окремих платежів (надходжень). Дана сума виражається такою формулою:

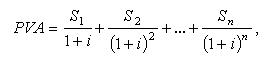
де PVA — теперішня вартість грошей, що повинна бути отримана.

● Приклад 11. Теперішня вартість ануїтета

Корпорація розраховує отримати наступні грошові потоки від вкладення інвестицій: рік 1 — $3000, рік 2 — $4000, рік 3 — $5000, рік 4 — $6000. Необхідна ставка прибутковості інвестицій — 12%. Визначте теперішню вартість грошових потоків від інвестицій.

Розв’язання. Використовуємо формулу (1.24) для визначення теперішньої вартості грошових потоків:

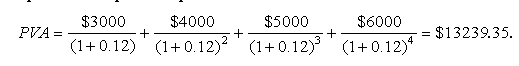
Теперішня вартість грошових потоків від інвестицій дорівнює $13239.35. (індекси: S1 = S2 = ... = Sn = S1)

Якщо ми припустимо, що S1 = S2 = ... = Sn = S, то сума PVA є не чим іншим, як добутком величини S на суму n членів геометричної прогресії зі знаменником і першим членом

● Приклад 12. Теперішня вартість ануїтета

Корпорація розраховує отримувати грошові надходження від впровадження нового проекту $5000 щорічно упродовж 10 років. Знайдіть теперішню вартість грошей, яку отримає корпорація, якщо ставка дисконта 10%.

Розв’язання. Використовуємо формулу (1.25) для визначення теперішньої вартості грошових потоків:

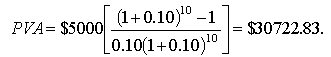
● Приклад 13. Відновлення капіталу

Позичальнику потрібні $30000 для подальшого інвестування. Банк надає позичку на 20 років під 8% річних з рівними щорічними платежами в кінці року. Знайдіть суму, яку повинен сплачувати позичальник у кінці кожного року.

Розв’язання. Використовуємо формулу (1.25) для визначення суми S, яку повинен сплачувати позичальник у кінці кожного року:

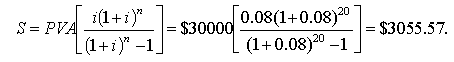
Позичальник повинен сплачувати щорічно $3055.57 упродовж 20 років, щоб повернути банку $30000 і проценти.

Перпетуїтет — це ануїтет або серія періодичних платежів, що тривають нескінченно. Якщо n прагне до нескінченності, то з рівняння (24) отримаємо, що границя PVA дорівнює 1/i.Тоді:

PV = P/i, (1.29)

де PV — теперішня вартість перпетуїтета;

P — річний платіж;

i — процентна ставка.

● Приклад 14. Теперішня вартість перпетуїтета

Якщо річна процентна ставка дорівнює 10%, то якою буде теперішня вартість перпетуїтета $1000?

Розв’язання. Використовуємо формулу (1.29) для визначення теперішньої вартості перпетуїтета PV:

PV = P/i = $1000/0.10 = $10000.

Теперішня вартість перпетуїтета дорівнює $10000.

Основні терміни: майбутня вартість грошей; теперішня вартість грошей; прості проценти; складні проценти; строк збільшення первісної суми інвестицій в N разів; ефективна процентна ставка; безперервні проценти; ануїтет; майбутня вартість авансового ануїтета; майбутня вартість звичайного ануїтета; процентний фактор майбутньої вартості ануїтета; фонд відшкодування; теперішня вартість ануїтета; процентний фактор теперішньої вартості ануїтета; відновлення капіталу; теперішня вартість перпетуїтета.