Економічний ризик: ігрові моделі (2002)

Правила прийняття рішень в умовах невизначеності, конфліктності та зумовленого ними ризику базуються на різних концепціях. Найбільш відомою, достатньо дослідженою й широко використовуваною в теорії та на практиці є концепція теорії гри та статистичних рішень.

Теорія гри — це розділ сучасної математики, в якому вивчаються математичні моделі прийняття рішень в умовах невизначеності, конфліктності, тобто в ситуаціях, коли інтереси сторін (гравців) або протилежні (у випадку антагоністичних ігор), або не збігаються, хоча й не протилежні (у випадку ігор з непротилежними інтересами). Засновниками теорії гри є американські вчені Джон (Януш) фон Нейман (1903—1957), угорського походження, та Оскар Моргенштерн (1902—1977), австрійського походження. У другій половині 40-х років ХХ ст. вони спробували за допомогою математики описати характерні для ринкової економіки явища конкуренції як деяку “гру”.

Гра — це формалізований опис (модель) конфліктної ситуації, що включає чітко визначені правила дій її учасників, які намагаються отримати певну перемогу шляхом вибору конкретної (в певному сенсі — найкращої) стратегії поведінки. Суб’єкт прийняття рішення (СПР) називається гравцем, а цільова функція — платіжною функцією. У грі можуть брати участь кілька гравців, причому деякі з них можуть вступати між собою в постійні або тимчасові коаліції (спілки). У випадку утворення коаліцій гра носить назву “коаліційної”. Гра двох осіб називається парною грою.

Кожен гравець приймає такі рішення, тобто вибирає таку стратегію поведінки, щоб максимізувати свій виграш або мінімізувати програш. При цьому він не знає, яких стратегій дотримуватимуться інші гравці. Отже, кожен гравець приймає свої рішення в умовах невизначеності, а результат обраної ним стратегії залежить від поводження всіх учасників гри.

Питанням оптимальності щодо функціонування і розвитку економічних систем в умовах невизначеності, конфлікту та породженого ними ризику посвячена велика кількість наукових праць [3, 4, 12, 16, 20—29, 31, 33—40, 43, 45, 47, 59, 64, 72, 84, 93, 96—100, 104, 107, 108, 115, 117]. Це викликано різноманітністю прояву чинників невизначеності та конфлікту в реальних процесах та явищах.

Для дослідження статистичних моделей в умовах невизначеності, конфліктності та породженого ними ризику використовують схему гри з економічним середовищем, складовими якої є:

перший гравець ― суб’єкт керування (СПР), вибір стратегії поведінки якого базується на множині S = si;...sm рішень (чистих стратегій), одне з яких йому необхідно прийняти;

другий гравець — економічне середовище, яке може знаходитися в одному з n попарно несумісних станів Өj, які утворюють множину Ө = (Өj; ...; Өn) , й один з яких обов’язково настане;

відсутність у СПР апріорної інформації про те, в якому зі своїх станів знаходитиметься економічне середовище (яке рішення прийме другий гравець);

точне знання СПР функціонала оцінювання (матриці) F = (fkj: k = 1,...m, j = 1,...n) , елемент fkj якого є кількісною оцінкою ефективності результату діяльності СПР у випадку вибору ним стратегії sk за реалізації стану економічного середовища.

Запропонована схема моделювання процесу прийняття раціонального рішення допускає таку інтерпретацію: другий гравець парної гри замінюється випадковим вибором або неусвідомлено приймаючим свої рішення економічним середовищем, а сама ситуація прийняття рішення характеризується функціоналом оцінювання F, який називають також (статистичною) матрицею гри, або платіжною матрицею.

Формально ситуація прийняття рішення згідно з теоретико-ігровою концепцією описується трійкою множин:

{S; Ө; F}.

Цікавою, з практичної точки зору, є змішана ігрова модель, коли множина стратегій суб’єкта керування S є дискретною і може набувати скінченної кількості варіантів, а множина станів економічного середовища Q — неперервною. В цьому випадку ситуація прийняття рішень характеризується сукупністю функцій:

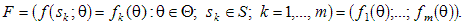
Доречно виділити творчу та формальну складові щодо побудови теоретико-ігрової моделі. Основні етапи творчої складової такі:

формування множин рішень першого та другого гравців, тобто перелік чистих стратегій СПР і станів економічного середовища (“природи”);

визначення та формалізація основних показників ефективності та корисності, побудова платіжної матриці F;

визначення (ідентифікація) наявної інформаційної ситуації, яка характеризує поведінку економічного середовища;

вибір критерію прийняття рішення з множини критеріїв, характерних для ідентифікованої інформаційної ситуації;

прийняття згідно з вибраним критерієм рішення із сукупності чистих або змішаних стратегій, якщо використання останніх можливе.

Окрім творчої складової, процес прийняття рішення в умовах невизначеності, конфліктності та зумовленого ними ризику вимагає досконалого володіння формальною складовою. Суть останньої полягає у використанні математичного апарату та виконанні розрахунків щодо показників ефективності, на основі яких будується функціонал оцінювання F, а також розрахунків щодо пошуку оптимальної (раціональної) стратегії або множини оптимальних (раціональних) стратегій згідно з вибраним критерієм оптимальності.