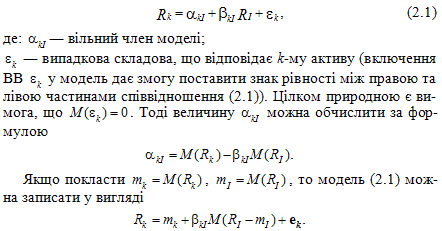Економічний ризик: ігрові моделі (2002)

Аналіз та оцінка співвідношення ризику та доходу відіграють ключову роль під час прийняття рішень щодо інвестицій (у цінні папери тощо). Одним із основних показників, використовуваних під час аналізу фінансових ризиків, є показник систематичного ризику — чи коефіцієнт чутливості «бета» (β) [75, 112]. Цей коефіцієнт називають також показником недиверсифіковуваного ризику.

Показник β характеризує змінюваність доходів певного активу відносно доходів «середньозваженого», повністю диверсифікованого портфеля, котрим, в ідеальному випадку, є весь ринок цінних паперів.

Уважають, що показник систематичного ризику для «середньої» акції, динаміка доходів якої збігається з динамікою ризику ринку цінних паперів у цілому (вимірюється за будь-яким фондовим індексом I), дорівнює одиниці (βср = βП = 1).

Розрахунком показників систематичного ризику для акціонерних фірм займаються консалтингові та інвестиційні компанії, фінансово-кредитні заклади тощо. Значення цих показників регулярно публікуються у фінансовій періодиці (західній) і широко використовуються для аналізу якості інвестиційних проектів.

Приклад 2.4. Згідно з розрахунками консалтингової компанії коефіцієнти систематичного ризику акцій фірм відповідно мають значення β1I = 1,35 та β2I = 0,9. Як зміняться індекси акцій цих фірм, якщо загальноринковий індекс збільшився на 20 пунктів?

Розв’язання. Значення коефіцієнта β1I = 1,35 свідчить про більший ступінь ризику щодо придбання акції першої фірми порівняно зі ступенем ризику ринку цінних паперів в цілому приблизно на:

(β1I – 1) Ч 100 % = (1,35 – 1) Ч 100 % = 35 %.

Індекс акцій першої фірми збільшився на 20β1I = 20Ч 1,35 = 27 (пунктів). Ризикованість вкладень в акції другої фірми на 10% менша ступеня ризику ринку:

(β1I – 1) Ч 100 % = (0,9 – 1) Ч 100 % = –10 %.

Індекс акцій другої фірми збільшився на 20β1I = 20Ч 0,9 = 18 (пунктів).

Відповідь: Індекси акцій цих фірм збільшаться на 27 та 18 пунктів відповідно.

Величина βkI ― коефіцієнт систематичного ризику k-го активу характеризує щільність зв’язку між біржовим курсом акції k-ї компанії та загальним станом ринку, що відображається ринковим індексом І, визначається за формулою:

Багаторічні спостереження показали, що норми прибутку більшості акцій залежать, в основному, від одного чинника ― загальноринкового індексу І. Наприклад, від широко відомого S&P 500, причому ця залежність описується лінійною економетричною моделлю (однофакторна модель Шарпа):