Економічний ризик: ігрові моделі (2002)
Додаток до розділу 3

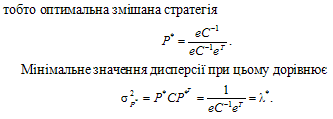
2. Доведення теорем





3. Метод множників Лагранжа. Матриця Гессе

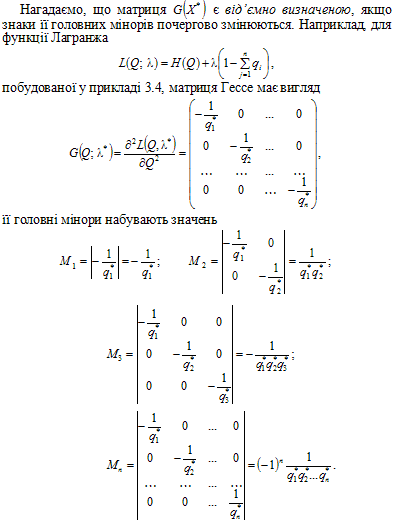

Наприклад, якщо деякий множник Лагранжа дорівнює нулю, то невеликі зміни збурення відповідної константи обмежень не впливатимуть суттєво на оптимальне значення цільової функції. Особливо важливою є інтерпретація множників Лагранжа в задачах раціональної економічної діяльності. В задачах розподілу ресурсів цільова функція має розмірність вартості, тобто ціни, помноженої на обсяг продукції (таким, наприклад, є прибуток, виручка, витрати), а з допомогою обмежень установлюється певне значення деякої кількісної характеристики (наприклад, обсягів витрат). Оскільки в таких задачах з допомогою відповідного множника Лагранжа вимірюється чутливість величини, що має розмірність вартості, щодо зміни певної кількості, то він (цей множник) має розмірність ціни. Множники Лагранжа часто називають тіньовими цінами (відповідних ресурсів).
4. Позначення, використані в розділі 3


