Економічний ризик: ігрові моделі (2002)
6.4.2. Теоретико-ігрова модель вибору структури портфеля за невідомого розподілу ймовірності

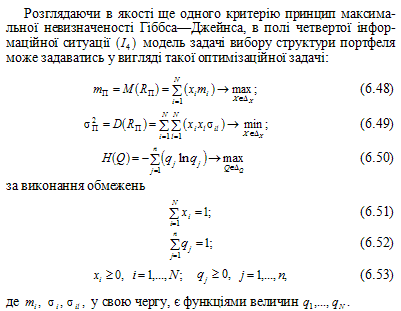
Як зазначалось раніше (у розділі 4) під час розв’язання багатокритеріальних задач (задача (6.48)—(6.53) є трикритеріальною) слід відмовитись від пошуку рішення, яке було б найкращим одночасно згідно з усіма критеріями, оскільки воно просто може й не існувати. А це означає, що пошук прийнятного (компромісного) рішення слід здійснювати серед ефективних портфелів, для яких будь-яке інше рішення, що є кращим згідно з одним критерієм, обов’язково буде гіршим з позиції інших (принаймні, хоча б одного з них).

Отже, як бачимо, процес побудови множини ефективних портфелів пов’язаний із суттєвими труднощами, а тому безпосереднє використання означення 6.3 не завжди може бути конструктивним. Спрощення у цьому плані можна досягнути шляхом уведення до розгляду портфелів, що визначаються на основі наведеної нижче дефініції.

Вимоги, наведені в означенні6.4, є досить жорсткими, але можна вказати випадок, коли існує портфель, що є ефективним згідно з концепцією Марковіца для будь-якого розподілу ймовірності, а визначення його структури зводиться до парної гри з нульовою сумою.

Приклад.6.4. Наявні активи п’яти видів, можливі значення норм прибутків яких залежать від стану ринку (економічного середовища). Визначити структуру ефективного портфеля згідно з концепцією Марковіца, якщо ринок може перебувати лише у двох станах, імовірності настання яких невідомі, і при цьому матриця норм прибутків активів:




Використаємо зазначені результати для знаходження структури ефективного портфеля.
Приклад6.5. Наявні активи двох видів, можливі значення норм прибутків яких залежать від станів ринку. Визначити структуру ефективного портфеля згідно з концепцією Марковіца для четвертої інформаційної ситуації (I4), якщо ринок може набувати шести станів, імовірності настання яких невідомі. Норми прибутків цих двох активів, відповідно до станів ринку, задаються матрицею: