Економічний ризик: ігрові моделі (2002)

Наведемо задачу, розглянуту в [34,81]. Інвестор взяв у борг гроші під 1,5% з метою інвестування цих засобів в акції різних компаній. Наявні два види акцій, норми прибутку яких є випадковими величинами і залежать від станів економічного середовища (випадкових обставин). На ринку можуть мати місце тільки дві ситуації: перша (Ө1) з імовірністю q = 0,2 і друга (Ө2)— з імовірністю q = 0,8.

Акції реагують на ці ситуації (стани економічного середовища) по-різному: курс акцій першого виду (s1) у першій ситуації зростає на 5%, а в другій — на 1,25%; курс акцій другого виду (s2) у першій ситуації падає на 1%, а в другій — зростає на 2,75%.

Необхідно найкращим чином розподілити наявний капітал між цими активами. Попередньо проаналізуємо ці акції з позиції таких їх характеристик, як сподівана норма прибутку (математичне сподівання норми прибутку) та величина ризику (дисперсія норми прибутку). Обчислимо ці характеристики:

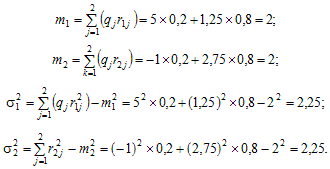
Хоча значення сподіваних норм прибутку і ризиків збіглися (m1 = m2 = 2; σ21 = σ22 = 2,25), у випадку інвестування всього капіталу в акції одного виду перевагу слід віддати акціям другого виду. На користь такого вибору свідчать такі міркування. У випадку придбання акцій тільки першого виду банкрутство інвестора може відбутися за настання другої ситуації (1,25 < 1,5), тобто з імовірністю q2 = 0,8. Якщо ж придбати акції тільки другого виду, то банкрутство інвестора відбудеться вже у випадку настання першої ситуації (-1 < 1,5,) тобто з імовірністю q1 = 0,2. Оскільки q1 = 0,2 < 0,8 = q2, то ризик банкрутства в разі інвестування лише в акції другого виду менший за ризик банкрутства в разі інвестування лише в акції першого виду. Але, як бачимо, повністю уникнути банкрутства при інвестуванні всього капіталу в акції другого виду неможливо.

Дослідимо ефект диверсифікації, тобто ефект від розподілу грошових ресурсів між обома активами в найбільш вигідних і безпечних пропорціях. Нехай x1 — частка капіталу, інвестованого в акції першого виду, тоді x2 = 1 - x1 — частка капіталу, інвестованого в акції другого виду, вектор X = (x1; x2) — структура портфеля акцій. Знайдемо характеристики портфеля. Його сподівана норма прибутку

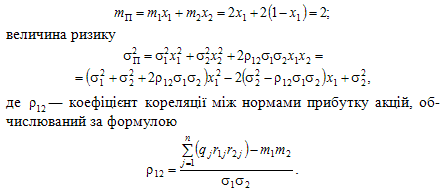
З урахуванням того, що σ1 = σ2 = 1,5; p12 = -1 (тобто має місце абсолютно від’ємна кореляція), отримуємо, що величина ризику портфеля, як функція від частки x1, обчислюється формулою

σП2 = 9х12 – 9х1 + 2,25.

У даному випадку найкращим портфелем слід уважати портфель з найменшою величиною ризику. Позначимо його структуру через X = (x1; x2). При x1 функція досягає свого мінімального значення. Згідно з необхідною умовою екстремуму функції для знаходження x1 слід скористатися рівнянням

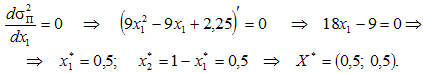
Отриманий результат вказує на те, що розподіл капіталу на рівні частки (по 50%) між акціями обох видів дає змогу, в певному сенсі, позбутися ризику (σП2 = 0). Окрім того, за такого розподілу грошей інвестору не загрожує банкрутство, оскільки для будь-якого стану економічного середовища норма прибутку портфеля, що має структуру X = (0,5; 0,5), становить 2% > 1,5% (переконайтесь у цьому самостійно).

Із задачею побудови оптимального портфеля цінних паперів у даному випадку мають безпосередній зв’язок дві матриці:

Розглянемо парну гру з нульовою сумою, що визначається матрицею С. Легко переконатись у тому, що ця гра не має сідлової точки, а її розв’язком є пара оптимальних змішаних стратегій sp та qQ, яким відповідають вектори P = Q = (0,5; 0,5) = X.

При цьому ціна гри V = 0 = (σП)2.

Парна гра з нульовою сумою, що визначається матрицею F, також не має сідлової точки і при цьому оптимальній змішаній стратегії першого гравця (інвестора) відповідає вектор P = (0,5; 0,5) = X. Ціна цієї гри V = 2.

Збіг оптимальних змішаних стратегій, що є розв’язком обох розглянутих ігор, не випадковий. Відповідні результати, що підтвержують цю закономірність, будуть отримані у розділі 6, в якому досліджуються питання використання теорії ігор для оптимізації структури портфеля.