Економічний ризик: ігрові моделі (2002)
1.5.6. Ігрова модель задачі побудови портфеля активів
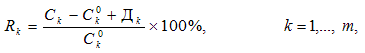
де: C k0 — ціна активу на початок даного періоду Ck– ціна активу (випадкова величина) на кінець даного періоду; Дk– дивіденди (теж випадкова величина), нараховані протягом даного періоду. Конкретне значення норми прибутку k-го активу залежить від стану економічного середовища, тобто визначається ситуацією, що склалася на ринку. Розмірність множини Θ станів економічного середовища може бути довільною, але ми вважатимемо її скінченною і рівною n, тобто Θ = (Ө1;...; Өn). Кожному стану ринку Өj поставимо у відповідність імовірність настання його qi. Всі ці ймовірності згрупуємо у вектор Q = (q1;...; qn). Очевидно, що компоненти вектора Q мають задовольняти співвідношенням.
Уважається, що можливі значення норми прибутку k-го активу (k = 1,... m) для всіх можливих станів ринку Өj = (1,…n) є відомими і відображаються випадковою величиною Rk = (rk1;…; rkn), тобто актив k-го виду приносить rk1 одиниць прибутку з розрахунку на кожну одиницю вкладень, якщо економічне середовище знаходитиметься в своєму j-му стані. СПР має можливість інвестувати свої ресурси більш як в один актив, утворити портфель, тобто розподілити свої ресурси між різними активами в найвигіднішій і безпечній пропорції. А тому інвестор (СПР) хоче оптимізувати структуру портфеля X = (x1;…;xm) шляхом визначення оптимальних розмірів часток xk (k = 1,…m), які відповідають вартості активів кожного виду в загальному обсязі інвестованих у портфель ресурсів.
У своїй моделі Марковіц відштовхується від того, що інвестор для прийняття інвестиційних рішень в якості критеріїв оптимальності використовує лише дві характеристики активів та їх портфелів: сподівану норму прибутку (у формі математичного сподівання) та величину ризику (у формі дисперсії).
Вибір цих кількісних характеристик у якості критеріїв оптимальності дає можливість розглядати задачу побудови портфеля як двокритеріальну. До речі, інвестор схильний вкласти весь свій капітал лише в актив одного виду, якщо цей актив, порівняно з будь-яким портфелем, буде найкращим за обома цими критеріями одночасно, тобто матиме найбільшу сподівану норму прибутку та найменшу величину ризику.

Ураховуючи зроблені раніше викладки, можна стверджувати, що задача оптимізації структури портфеля пов’язана з декількома матрицями, кожну з яких можна вибрати в якості функціонала оцінювання статистичної гри. Розглянемо функціонал оцінювання
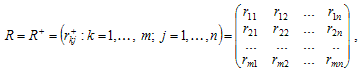
у k-му рядку якого розміщено можливі значення норми прибутку Rk активу k-го виду, а в j-му стовпчику — величини норм прибутків активів усіх видів, що відповідають j-му стану ринку (k = 1,…, m; j = 1,…, n). Змішану стратегію першого гравця, якій відповідає вектор P = (p1;…; pm) у грі, що визначається матрицею R, можна тепер інтерпретувати як портфель, а ймовірність pk — як частку капіталу, інвестованого в актив k-го виду (k = 1,…, m). Розв’язок гри в чистих стратегіях відповідатиме «однорідному» портфелю, тобто портфелю, складеному тільки з активів одного виду. А вибір розв’язку гри у змішаних стратегіях вказує на факт формування портфеля з різних активів. Як це показано в [38, 97—100], за виконання певних умов оптимальна змішана стратегія з вектором P = (p1;…; pm) відповідає ефективному портфелю.
Оптимізація структури портфеля відіграє особливу роль у сучасній економічній теорії та практиці. Можна стверджувати, що будь-яка економічна проблема зводиться до задачі найкращого розподілу ресурсів (матеріальних, фінансових, трудових тощо), наявних у розпорядженні СПР (інвестора) між активами різних видів.