Економічний ризик: ігрові моделі (2002)
2.3.1. Міра ризику як векторна величина
Отже, оцінюючи ризик економічного об’єкта (системи), суб’єкт ризику, як правило, цікавиться низкою показників, які відбивають різні грані невизначеності, конфлікту та породженого ними ризику. На наш погляд, кількісна міра ризику — це вектор W = (w1; w2;…) де wi (I = 1, 2,…) окремі показники (компоненти) міри ризику. Частина з них має об’єктивну природу (дисперсія, семиваріація, коефіцієнт варіації тощо); решта компонент цього вектора є суб’єктивними оцінками ступеня ризику, оскільки вони залежать від ставлення суб’єкта ризику до невизначеності, конфліктності.
На даний час теорія ризику та економічна практика виробили низку окремих показників кількісної оцінки ступеня ризику, серед яких фінансові коефіцієнти широко використовувані, наприклад, у банківській, страховій справі, в проектному менеджменті. Низку показників ступеня ризику поділяють на такі, що характеризують міру ризику в абсолютному чи у відносному вираженні. Існують також інші класифікаційні ознаки щодо вибору компонент вектора W. Наголосимо, що цей вибір залежить від сфери економічної діяльності (об’єкта, що аналізується, системи тощо), від цілей дослідження (аналізу, оцінювання, прийняття рішень), від прийнятої системи гіпотез, від інформаційної ситуації (вид, тип невизначеності та конфлікту), а також від його екстравертності чи інтравертності тощо.
Для прикладу звернемося до прогнозування і планування податкових надходжень до державного та місцевого бюджетів. Розглянемо категорію податкового ризику як одну із складових багаточинникової оцінки стійкості та надійності прийняття рішень щодо обсягів планових податкових надходжень на підґрунті їх прогнозованих обсягів.
Відомо, що прогнозування будь-якого економічного показника пов’язане з похибкою прогнозу. Величина похибки визначає ступінь ризику планів (рішень), які ґрунтуються на прогнозованих економічних показниках. У статистичному моделюванні та прогнозуванні вводяться та аналізуються такі поняття, як середній та емпіричний ризик. За показник ступеня середнього ризику, зокрема, обирається математичне сподівання квадрата різниці між розрахунковими і фактичними значеннями прогнозованого економічного показника. Мінімізація ступеня середнього ризику дає змогу найбільш правдоподібно виявити закономірності та реально існуючі суттєві взаємозв’язки. При порівнянні альтернативних математичних моделей прогнозування кращою можна вважати ту з них, якій відповідає мінімальне значення низки відповідних показників ступеня ризику, і, зокрема, значення ступеня середнього ризику. Це стосується і моделей прогнозування обсягів податкових надходжень.
На підставі прогнозованих обсягів податкових надходжень визначають плановим обсяг, який приймається дещо меншим, аніж середнє значення прогнозованого обсягу. На цьому етапі необхідно, крім об’єктивної складової міри ризику, ввести й суб’єктивну складову, за яку доречно обрати ймовірність недовиконання запланованого обсягу податкових надходжень, обчислену на підґрунті їх прогнозованого обсягу. Очевидно, що величину оцінки ступеня ризику (ймовірність) недовиконання планового обсягу надходжень необхідно зробити якомога меншою. Відсоток недовиконання обсягів планових податкових надходжень, у разі встановлення цих обсягів, може розглядатися як ще один показник суб’єктивної оцінки міри ризику. Він задається нормативно, залежно від ставлення суб’єкта прийняття рішення до ризику на підґрунті обсягів прогнозованих величин, що задаються певним інтервалом значень і де враховується ризик того, що прогнозована величина може сягнути за межі цього інтервалу.
Доречно також ввести як один із компонентів векторної оцінки міри податкового ризику показник ступеня ризику невикористаних можливостей, який характеризує міру відхилення планових обсягів податкових надходжень від максимально можливого прогнозованого обсягу надходжень, одержаного на базі використання адекватних математичних моделей і методів. Усі ці складові міри податкового ризику доцільно використовувати системно, комплексно.
У низці наукових праць домінує думка, що показником ризику може слугувати певна скалярна величина (індикатор ризику). В деяких випадках це правильно, але далеко не завжди. Тому прагнення синтезувати такий індикатор, здійснюючи певну згортку окремих показників ризику, не в усіх випадках сприяє правильному оцінюванню його та врахуванню під час аналізу проектів. Наприклад, у прогнозуванні економічних показників використовується низка критеріїв адекватності та точності прогнозу. Для здійснення інтервального прогнозу вектор ризику W можна встановити як такий, що складається з трьох параметрів: w1 = σ — середньоквадратичне відхилення прогнозованої величини; w2 = p — імовірність того, що ця випадкова величина може сягати за межі певного прогнозованого інтервалу; w3 = CV — коефіцієнт варіації. У даному випадку параметри вектора W (σ; p; CV) немає підстав інтегрувати, здійснюючи їх згортку. Прогнозована величина знаходиться в інтервалі m ± kσ де m — математичне сподівання прогнозованого показника; k знаходиться з оцінки закону розподілу прогнозованого показника (як випадкової величини), а також беручи до уваги задане (суб’єктивне) значення компоненти ризику w2 = p = p*. Коли немає підстав для оцінки закону розподілу, можна скористатися нерівністю Чебишева.
Коефіцієнт варіації у ряді випадків виступає в ролі індикатора для обчислення ефективних (несприятливих) значень певного економічного показника:
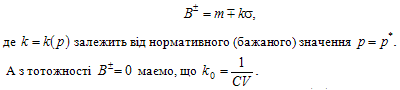
Необхідно також наголосити, що далеко не завжди виконуються умови, коли економічні показники (які ми трактуємо як випадкові величини) мають симетричний та, більш того, нормальний закон розподілу. У цих випадках за базу слід обрати моду, а одним з показників ризику може бути модальне семiквадратичне відхилення.
Крім того, в ряді випадків як альтернатива теорії ймовірностей усе частіше використовується теорія нечітких множин, якщо вона адекватно відбиває даний вид невизначеності. Тоді будуються свої показники оцінки ступеня ризику та відповідний вектор (W) міри ризику. Зазначимо, що для оцінювання міри ризику перспективним є тензорний аналіз, який дає змогу адекватно вимірювати ризики і приймати правильне рішення щодо зниження його ступеня.