Економічний ризик: ігрові моделі (2002)

Якщо в полі інформаційної ситуації I2 чи I3, чи I4 вдалося знайти точкову оцінку Q = (q1;…; qn) невідомого розподілу ймовірності Q = (q1;…; qn) станів економічного середовища (сценаріїв), то на підґрунті Q можна скористатися будь-яким критерієм прийняття рішень, що є характерним для I1. Наприклад, критерієм мінімальної дисперсії функціонала оцінювання (3.14).

За невідомого розподілу ймовірності Q = (q1;…; qn) станів економічного середовища оцінка Байєса Bp (3.13) та дисперсія σp2 (3.14) є функціями m + n змінних pk(k = 1,…, m) та qj(j = 1,…, n). Тоді пошук оптимальної змішаної стратегії sp* СПР зводиться до розв’язання задачі на умовний екстремум, де в якості цільової функції можуть використовуватися такі критерії (за умови, що F = F+, P → ∆p, Q → ∆Q):

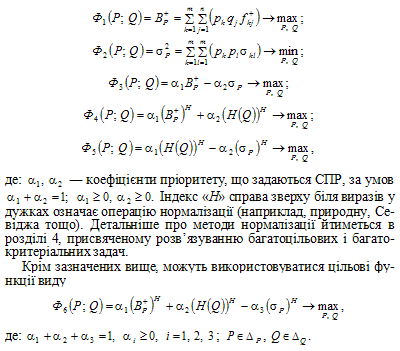
Як бачимо, наведені цільові функції можуть об’єднувати декілька показників (наприклад, математичне сподівання Bp, дисперсію σp2 та ентропію Шеннона H(Q)). Детальніше такого виду об’єднувальні критерії розглядатимуться в розділі 4.

За виконання умов теореми 3.1 у полі цих інформаційних ситуацій можна використовувати ігровий підхід для пошуку оптимальної змішаної стратегії СПР. У багатьох випадках знайдена ігровим методом оптимальна змішана стратегія СПР задає шукану точку екстремуму відповідної цільової функції за накладених обмежень.