Економічний ризик: ігрові моделі (2002)
5.6.9. Ігровий підхід до методу аналізу ієрархій
Для висвітлення суті ІМАІ повернемося до прикладу 5.7. Згідно з його умовою експерти оцінювали елементи ієрархічної моделі виходячи з певного інтуїтивно ними зафіксованого (прогнозованого) стану економічного середовища. Очевидно, що оцінювання експертів можна зробити ефективнішими, якщо виходити з позиції теоретико-ігрової моделі і ввести до розгляду множину станів економічного середовища Θ = (Ө1;…; Өn). Це виправдано тим, що побудова матриці попарних порівнянь для кожного стану економічного середовища є значно простішою, а тому й точнішою процедурою, порівняно з використовуваною в МАІ.
Приклад 5.8. Побудувати модель множини станів економічного середовища для прикладу 5.7 виходячи з того, що у майбутньому (за період, на який надається кредит):
ціни на дорогоцінні метали не зміняться (a);
курс іноземної валюти може впасти на певну величину (β1) або піднятися (β2);
вартість цінних паперів може зменшитися незначно (γ1) або суттєво (γ2);
вартість нерухомості практично не змінюється (ξ).
Розв’язання. Можна виділити такі стани економічного середовища:
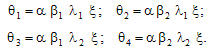
Очевидно, що у випадку, коли економічне середовище буде знаходитись у стані Ө2 (найбільш сприятливому для СПР), то за порівняння елементів-«нащадків» відносно «батьківського» елемента оцінки експерта можуть суттєво відрізнятися від оцінок, що їх він дасть тим же об’єктам у випадку Ө3 (найменш сприятливому для СПР стані).
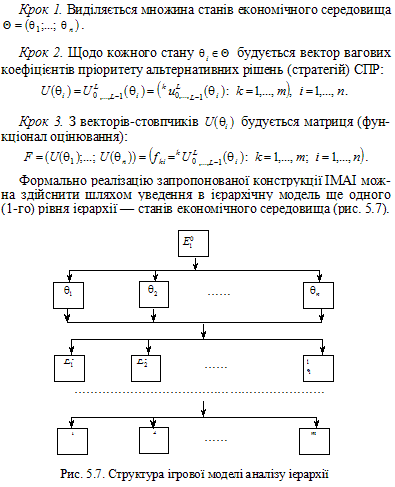

За необхідності згортання матриці F можна реалізувати на основі оператора ZF, який використовувався для побудови ієрархічних моделей (розділ 4, пункт 4.7.9).
Якщо ж розподіл імовірності станів економічного середовища невідомий, то його оцінювання можна здійснити в полі наявної інформаційної ситуації за допомогою методів, запропонованих раніше (розділ 4). Крім того, можна скористатися методологією, притаманною МАІ, а саме, побудувати матрицю попарних порівнянь станів економічного середовища і на її основі обчислити вектор вагових коефіцієнтів пріоритету щодо цих станів. Отриманий вектор можна надалі використовувати в якості оцінки розподілу ймовірності станів.
ІМАІ можна реалізувати й іншим шляхом, коли кожне порівняння елементів-«нащадків» відносно «батьківського» елемента здійснюється послідовно для кожного стану економічного середовища. У результаті таких n процедур порівнянь між собою елементів-«нащадків» отримуємо n матриць попарних порівнянь. Отримані матриці розміщуються паралельно одна одній, утворюючи при цьому паралелепіпед (вісь абсцис — рядки матриць, вісь ординат — їх стовпчики, вісь аплікат — стани економічного середовища).
Тоді перетворення, аналогічні тим, що проводилися для реалізації МАІ, необхідно здійснити послідовно для кожної матриці паралелепіпеда. В результаті на кожному етапі синтезу будуть отримані матриці вагових коефіцієнтів пріоритету елементів певного рівня ієрархії. При цьому кожен рядок (вертикальної) матриці є паралельним осі абсцис і містить елементи вектора вагових коефіцієнтів пріоритету, що відповідає певному стану економічного середовища.
Результатом такого синтезу буде матриця вагових коефіцієнтів пріоритету рішень (стратегій) СПР. На основі аналізу цієї матриці можна визначити рейтинг рішень (стратегій) і, за необхідності, прийняти одне з них.
У [22, 30] для побудови матриць попарних порівнянь запропоновано використовувати апарат нечітких множин. Там же запропоновано до використання розпливчастий метод аналізу ієрархій (РМАІ), а також ігровий розпливчастий метод аналізу ієрархій (ІРМАІ). Підхід з позиції теорії нечітких множин для аналізу ієрархій використовується також у [5].