Економічний ризик: ігрові моделі (2002)
6.3.2. Концептуальні підходи до побудови множини портфелів
Необхідно прагнути розподілити вкладення між різними видами активів, а власне такими, що показали в минулому (за попередні періоди часу), по-перше, різну щільність зв’язку (кореляцію) із загальноринковими цінами (індексами) і, по-друге, незбіжну між собою фазу коливань норм прибутку (цін) усередині портфеля.
Управління портфелем — це планування, аналіз і регулювання структури портфеля, діяльність з його формування та підтримки з метою досягнення поставлених цілей за умови збереження необхідного ступеня його ризику та мінімізації витрат, пов’язаних з цим. (Нами в попередньому матеріалі було коротко охарактеризовано етапи інвестиційного процесу. Конкретний перелік операцій, які охоплює поняття «управління портфелем», наведено в [34, 55, 106].)
Розглянемо послідовність дій інвестора під час вибору оптимального, в певному сенсі, портфеля. Нагадаємо, що структура портфеля задається вектором X = (xi;…; XN), де xi ― відносна вага активу в портфелі або частка від усього початкового капіталу, інвестованого в актив і-го виду. Підхід Марковіца щодо прийняття інвестиційних рішень базується на аналізі сподіваних (середніх) значень і дисперсій (варіацій) випадкових величин — норм прибутку активів та їх портфелів. Саме ці числові характеристики і використовуються в якості критеріїв оптимальності під час вибору портфелів з наперед заданими властивостями.
У конкретних задачах можуть задаватися фінансові умови, що впливають на формування структури портфеля. Наприклад, виключення коротких позицій (класичні портфелі, структури яких мають лише невід’ємні компоненти), обмеженість зверху чи знизу обсягу окремої позиції тощо.
Розв’язання задачі вибору портфеля зі структурою, що відповідає заданим властивостям, можна починати з побудови множини ефективних (непокращуваних) портфелів. Якщо кожному портфелю поставити у відповідність точку, координатами якої є його числові характеристики (критерії), то математичною моделлю сукупності допустимих портфелів є (критеріальна) множина точок (на площині, в просторі), а моделлю сукупності ефективних портфелів — частина границі цієї множини. Так, у моделі Марковіца сукупність допустимих портфелів задається множиною точок у двовимірному просторі (на площині):

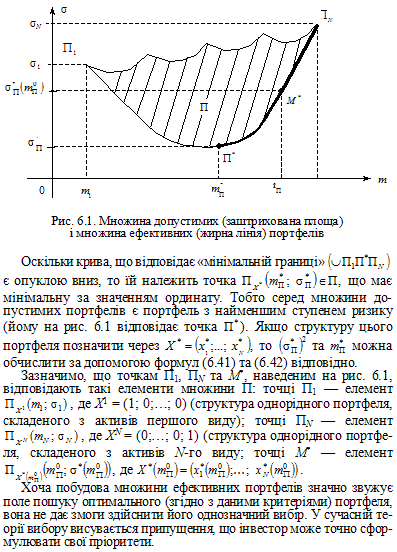
Сутність підходу до побудови математичної моделі множини ефективних портфелів полягає у тому, що фіксуються значення всіх кількісних показників (критеріїв) портфеля, крім одного, за незафіксованим показником відшукується оптимальне значення. Так, зафіксувавши в моделі (6.32)―(6.34) рівень сподіваної норми прибутку портфеля m = mП 0 = const і розв’язавши відповідну задачу мінімізації ризику портфеля, знаходимо величину σП* (тобто серед усіх портфелів, сподівана норма прибутку яких є фіксованою і становить mП 0 = const, знаходимо портфель, ступінь ризику якого досягає мінімального рівня σП*(mП0)). Портфелі, що мають числові характеристики mП 0 та σП*(mП0), належать множині ефективних портфелів. Марковіц показав, що у просторі « » множині ефективних портфелів відповідають точки, які належать неперервній, угнутій (опуклій вниз, рис. 6.1) кривій, складеній зі скінченої кількості кусків гіпербол і (можливо) прямолінійних відрізків.
На рис. 6.1 наведено геометричні образи: множина допустимих портфелів (множина П), якій відповідає заштрихована частина наведеної фігури; «мінімальна границя» — дуга П1П*N; множина ефективних портфелів — дуга П*П2. На рисунку: точці П1 відповідає обтяжений ризиком актив з числовими характеристиками т1 та 1, при цьому його сподівана норма прибутку (т1) є найменшою серед активів, що складають портфель; точці ПN відповідає обтяжений ризиком актив з числовими характеристиками тN та N, при цьому його сподівана норма прибутку (тN) є най-більшою серед активів, що складають портфель.
Детальніше процес побудови моделі множини допустимих портфелів досліджується в [32, 34, 112].


Підсумовуючи, зазначимо, що в останні десятиліття використання теорії портфеля значно розширилося. Все більший загал інвестиційних менеджерів, адміністраторів інвестиційних фондів використовують її методи на практиці. І хоча у сучасної теорії портфеля є противники, вплив її постійно зростає не тільки в науковій сфері, але й на практиці.