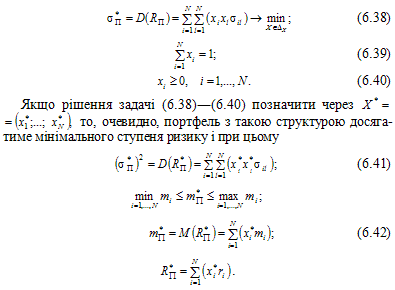Економічний ризик: ігрові моделі (2002)

Придбання акцій — безсумнівно є ризикованою фінансовою операцією. Вклавши свої ресурси в акції лише одного підприємства, інвестор стає заручником коливань їх курсової вартості на ринку цінних паперів. Але якщо інвестор розподілив свій капітал між декількома активами, то ефективність сформованого портфеля залежатиме від їх сумісного курсу, коливання якого значно менші. При цьому найважливішу роль відіграє вибір конкретної структури портфеля активів і він має базуватися на чітких розрахунках.

Як зазначалось раніше, в класичній теорії портфеля приймається гіпотеза щодо випадковості норм прибутків активів, а саме— що величини Ri є дискретними випадковими величинами (I = 1,…, N). Ця гіпотеза дозволяє використовувати в процесі побудови моделей методи теорії ймовірності та математичної статистики. Використовуючи введені позначення, класичну модель (концепцію) Марковіца задачі вибору портфеля з наперед заданими характеристиками можна подати в такому вигляді: серед елементів множини ∆x знайти елемент X* = (x1*;…; xN*), де xi* — частка капіталу, інвестованого в актив і-го виду (I = 1,…, N), щоб портфель зі структурою X* мав найбільшу сподівану норму прибутку та найменший ступінь ризику.

Згідно з наведеними означеннями допустимий портфель називається ефективним, якщо не існує іншого допустимого портфеля з не меншою сподіваною нормою прибутку і меншим ступенем ризику або з більшою сподіваною нормою прибутку і не більшим ступенем ризику. Ефективність портфеля означає його непокращуваність (непокращуваність числових характеристик). Щодо ефективного портфеля, то будь-який інший (незбіжний з ним) портфель має або більший ступінь ризику, або меншу сподівану норму прибутку. Такій властивості портфеля, як ефективність, можна надати наочної геометричної інтерпретації (рис. 6.1), якщо у двовимірному евклідовому просторі критеріїв (далі — критеріальний простір) «m–σ» вздовж однієї координатної осі відкладати сподівану норму прибутку портфеля, а вздовж другої— його ризик [32, 34, 81, 112].

Якщо скористатися принципом виділення основного критерію, то задачу пошуку ефективного портфеля (6.28)―(6.31) можна розглядати як такі дві задачі на умовний екстремум:

Зазначимо, що у випадку моделі Блека, коли відсутнє обмеження щодо знаку компонентів вектора Х, відповідна задача на умовний екстремум має рішення для будь-якого наперед заданого значення константи mП 0 При цьому чисто технічно реалізація алгоритма розв’язання задачі є значно простішою, ніж за розв’язання її з вимогою невід’ємності компонентів Х.

Розглянемо задачу мінімізації ризику портфеля на множині всіх допустимих портфелів (так звану задачу збереження капіталу [32]). Формально ця однокритеріальна задача задається співвідношеннями:

Портфель з мінімальним ризиком завжди існує в моделі Марковіца і в моделі Блека. Але в моделі Блека він, за досягнення мінімального ступеня ризику, може мати від’ємну сподівану норму прибутку. Якщо всі компоненти рішення задачі (6.38)―(6.39) є невід’ємними числами, то портфелі з найменшим ступенем ризику в обох моделях збігаються (мають однакову структуру).