Економічний ризик: ігрові моделі (2002)
7.4. Формування «валютного кошика»
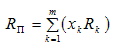
Як і у пункті 1.5.7, вважатимемо, що множина станів ринку іноземних валют (станів економічного середовища) дискретна зі скінченною кількістю елементів. Нехай т — кількість станів економічного середовища; rkj — значення, що приймає норма прибутку валюти k-го виду (k = 1,…, m) в умовах j-го стану економічного середовища (j = 1,…, n), при цьому значення rkj відомі. Тоді ситуацію прийняття рішення щодо створення «валютного кошика» можна охарактеризувати функціоналом оцінювання R+ = (rkj+ : k = 1,…, m; j = 1,…, n).
Аналогічно теорії Марковіца: сподівана норма прибутку валюти k-го виду — це математичне сподівання відповідної дискретної випадкової величини Rk:
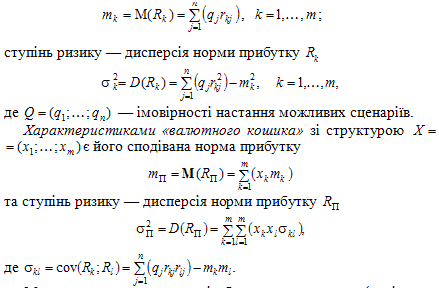
Математична модель задачі обрання оптимальної (раціональної) структури X = (x1;…; xm) «валютного кошика» має вигляд моделі задачі вибору оптимальної структури портфеля у полі відповідної інформаційної ситуації.
Як про це йшлося у розділі 5, існує низка добре відпра-цьованих методів розв’язування цих задач. Якщо матриця R = (rkj : k = 1,…, m; j = 1,…, n) не має сідлового елемента, то задачу вибору оптимальної структури «валютного кошика» можна звести до відшукання оптимальної раціональної змішаної стратегії відповідної гри двох осіб з нульовою сумою.

Це означає, що «валютний кошик» зі структурою P* = (p1*;…; pm*) є безризиковим, оскільки для будь-якого розподілу ймовірності щодо станів валютного ринку його дисперсія дорівнює нулю: σp*2 = D(Rp*) = 0. Таким чином, за цих умов ігровий підхід на базі платіжної матриці R = (rkj : k = 1,…, m; j = 1,… n) дозволяє знайти безризиковий «валютний кошик», причому в полі будь-якої інформаційної ситуації. Більш того, у ситуації I5, коли економічне середовище активно протидіє досягненню найбільшої ефективності рішень, формування суб’єктом ризику «валютного кошика» можливе лише на базі теоретико-ігрових методів.
Зазначимо, що у полі першої інформаційної ситуації (I1) формування «валютного кошика» з мінімальною дисперсією може ґрунтуватись також на розв’язанні парної гри з нульовою сумою, коли в якості платіжної матриці використовується коваріаційна матриця C = (σkj : k = 1,… m; j = 1,… n) (за виконання умов теореми 3.2).