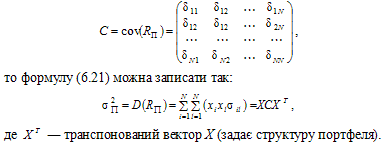Економічний ризик: ігрові моделі (2002)
6.2.2. Числові характеристики активів та їх обчислення
Ринок складається зі скінченної кількості активів, норми прибутків яких, для заданого періоду (інвестиційного горизонту), вважаються випадковими величинами.
Інвестор спроможний (наприклад, на основі статистичних даних) отримати оцінку сподіваних (середніх) значень норм прибутків активів, рівнів їх ризику та попарних коваріацій.
Інвестор може сформулювати будь-який допустимий (згідно з даною моделлю) портфель. Норма прибутку портфеля теж випадкова величина, для котрої інвестор може визначити числові характеристики.
Вибрані портфелі порівнюють тільки на основі двох характеристик: сподіваної норми прибутку, яка визначається шляхом обчислення математичного сподівання норми прибутку, та ступеня ризику, який визначається шляхом обчислення дисперсії норми прибутку або середньоквадратичного відхилення.
Індивідуальні пріоритети інвестора задаються функцією корисності, яка представляє собою узагальнений (комбінований) критерій порівняння портфелів (2.3.4.7). Вона залежить від сподіваної норми прибутку і ризику портфеля, а також від схильності (несхильності) інвестора до ризику.
З двох портфелів з однаковою нормою прибутку інвестор обов’язково віддасть перевагу портфелю, обтяженому меншим ризиком, з двох портфелів з однаковим ризиком — тому, що має більшу сподівану норму прибутку.
Отже, актив, обтяжений ризиком, характеризується двома показниками: сподіваною нормою прибутку (математичним сподіванням норми прибутку) і ступенем (рівнем) ризику, що визначається як дисперсія (середньоквадратичне відхилення) норми прибутку від її сподіваного значення.
Припустимо (з метою спрощення), що інвестор володіє певним початковим капіталом, тобто вартістю w, яку можна використати для інвестування у поточному періоді. Йому необхідно розподілити цей капітал між N активами. Як уже зазначалося, портфель — це набір активів. Такий набір можна задати шляхом впорядкування N чисел, тобто шляхом задання вектора:


Суть підходу Марковіца полягає в тому, що він запропонував розглядати норми прибутку активів і складених з них портфелів як випадкові величини. У моделі Марковіца це реалізовується таким чином: активу і-го виду ставиться у відповідність випадкова величина Ri = (I = 1,…, N), реалізації якої є нормами прибутку цього активу для вибраного інвестиційного горизонту (інвестиційного періоду). Значення норми прибутку активу і-го виду залежать від стану економічного середовища (ринку). Множина можливих станів ринку може складатися, в принципі, з будь-якої кількості елементів, зокрема й нескінченної (навіть бути континумом). Для спрощення викладок вважатимемо її скінченною.

Але оскільки йдеться про активи, обтяжені ризиком, то хоча б дві реалізації дискретної випадкової величини є різними (за значенням).
Якщо норму прибутку активу і-го виду задано у вигляді випадкової величини, то можна обчислити (оцінити) її числові характеристики, а саме: математичне сподівання, дисперсію, середньоквадратичне відхилення тощо.
Як уже зазначалося, в теорії Марковіца сподівана норма прибутку обчислюється як математичне сподівання відповідної випадкової величини. У дискретному випадку вона обчислюється за формулою:
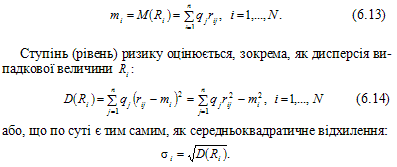
Портфель активів можна розглядати як своєрідний «складений» актив, а тому в якості його характеристик використовуються ті ж кількісні показники. При цьому приймається важлива угода про те, що інвестор свій вибір щодо інвестиційного рішення здійснює на основі аналізу сподіваної норми прибутку та ступеня ризику активів і їх портфеля. Якщо стратегія інвестора полягає в інвестуванні всього капіталу лише в актив одного виду, то цей актив повинен мати найбільшу сподівану норму прибутку і найменший ступінь ризику.
Як правило, актив, що має більшу сподівану норму прибутку, характеризується більшим рівнем ризику. В цьому випадку інвестор вибору одного активу протиставляє вибір портфеля з певної сукупності активів, намагаючись при цьому, по можливості, диверсифікувати (розподіляти) ризик з метою зменшення його рівня (редукції ризику). Ступінь можливості такої диверсифікації визначається характеристикою, що оцінює міру щільності лінійного взаємозв’язку між нормами прибутків активів, — з допомогою коваріації чи коефіцієнта парної кореляції. Для дискретних випадкових величин Ri та Rl коваріація обчислюється за формулою: